题目内容
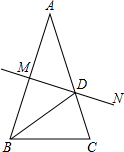 如图,已知AB=AC,AB的中垂线MN交AC于点D,交AB于点M,BD平分∠ABC.
如图,已知AB=AC,AB的中垂线MN交AC于点D,交AB于点M,BD平分∠ABC.
(1)求证:△ABC∽△BCD;
(2)求 的值;
的值;
(3)求cosA的值.
解:(1)证明:∵AB的中垂线MN交AC于点D
∴AD=BD
∴∠A=∠ABD
∵BD平分∠ABC
∴∠A=∠ABD=∠DBC,
又∵∠C是公共角
∴△ABC∽△BDC;
(2)根据(1)可得:AD=BD=BC
设AC=1,AD=x
∵△ABC∽△BCD
则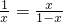 ,
,
解得 或
或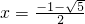 (不合题意,舍去)
(不合题意,舍去)
∴ ,
,
∴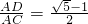 ;
;
(3)在Rt△AMD中,DM⊥AB
∴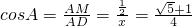 .
.
分析:(1)首先根据中垂线的性质得到AD=BD,接着得到∠A=∠ABD,而BD平分∠ABC,由此得到∠A=∠ABD=∠DBC,又∠C是公共角,然后利用相似三角形的判定定理即可证明△ABC∽△BCD;
(2)根据(1)可得AD=BD=BC,设AC=1,AD=x,然后利用相似三角形的性质得到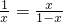 ,解方程求得
,解方程求得 ,然后就可以求出
,然后就可以求出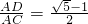 ;
;
(3)在Rt△AMD中,DM⊥AB,根据三角函数的定义即可解决问题.
点评:此题分别考查了相似三角形的性质与判定、垂直平分线的性质及三角函数的定义,综合性比较强,解题首先根据垂直平分线的性质构造相似三角形的条件,然后利用相似三角形的性质即可解决问题.
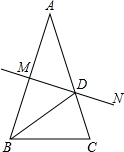
∴AD=BD
∴∠A=∠ABD
∵BD平分∠ABC
∴∠A=∠ABD=∠DBC,
又∵∠C是公共角
∴△ABC∽△BDC;
(2)根据(1)可得:AD=BD=BC
设AC=1,AD=x
∵△ABC∽△BCD
则
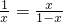 ,
,解得
 或
或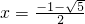 (不合题意,舍去)
(不合题意,舍去)∴
 ,
,∴
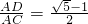 ;
;(3)在Rt△AMD中,DM⊥AB
∴
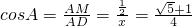 .
.分析:(1)首先根据中垂线的性质得到AD=BD,接着得到∠A=∠ABD,而BD平分∠ABC,由此得到∠A=∠ABD=∠DBC,又∠C是公共角,然后利用相似三角形的判定定理即可证明△ABC∽△BCD;
(2)根据(1)可得AD=BD=BC,设AC=1,AD=x,然后利用相似三角形的性质得到
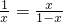 ,解方程求得
,解方程求得 ,然后就可以求出
,然后就可以求出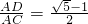 ;
;(3)在Rt△AMD中,DM⊥AB,根据三角函数的定义即可解决问题.
点评:此题分别考查了相似三角形的性质与判定、垂直平分线的性质及三角函数的定义,综合性比较强,解题首先根据垂直平分线的性质构造相似三角形的条件,然后利用相似三角形的性质即可解决问题.

练习册系列答案
相关题目
 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )| A、60° | B、90° | C、45° | D、120° |
 10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( )
10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( ) 26、如图,已知AB=AC,AD=AE.求证BD=CE.
26、如图,已知AB=AC,AD=AE.求证BD=CE. 2、如图,已知AB=AC,AD=AE,BD=EC,则图中有
2、如图,已知AB=AC,AD=AE,BD=EC,则图中有 如图,已知AB=AC,BC=CD=AD,求∠B的值.
如图,已知AB=AC,BC=CD=AD,求∠B的值.