题目内容
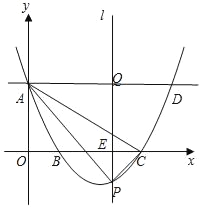
【题目】如图,在平面直角坐标系中,抛物线y=mx2﹣7mx+3与y轴交于点A,与x轴分别交于点B(1,0).点C(x2,0),过点A作直线AD∥x轴,与抛物线交于点D,在x轴上有一动点E(t,0),过点E作直线l∥y轴,与抛物线交于点P,与直线AD交于点Q.
(1)求抛物线的解析式及点C的坐标;
(2)当0<t≤7时,求△APC面积的最大值;
(3)当t>1时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)当x=1时,m﹣7m+3=1;(2)当t=7时,S△APC最大=![]() ,当t=3时,S△APC最大=
,当t=3时,S△APC最大=![]() ;
;
(3)存在,t=![]() 或
或![]() 或13.
或13.
【解析】分析:
(1)先将点B坐标代入抛物线解析式求出m,即可得出结论;
(2)分两种情况,利用面积和或差得出函数关系式,即可得出结论;
(3)分两种情况,利用相似三角形的性质得出比例式建立方程求解即可得出结论.
详解:(1)当x=1时,m﹣7m+3=1;
∴m=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x+3,
x+3,
当y=0时,0=![]() x2﹣
x2﹣![]() x+3,
x+3,
∴x=1或x=6,
∴C(6,0);
(2)由题意知,点P与点C不能重合,
∴t≠6,
∵A(0,3),C(6,0),
∴直线AC的解析式为y=﹣![]() +3,
+3,
∵E(t,0),
设直线AC与l的交点为F,
∴F(t,﹣![]() t+3),
t+3),
当0<t<6时,FP=﹣![]() t2+3t,
t2+3t,
∴S△APC=S△APF+S△PFC=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
当t=3时,S△APC最大=![]() ,
,
当6<t≤7时,S△APC=S△APF﹣S△PFC=![]() (t﹣3)2﹣
(t﹣3)2﹣![]() ,
,
当t=7时,S△APC最大=![]() ,
,
∴当t=3时,S△APC最大=![]() ;
;
(3)存在,
理由:在△AOB中,OA=3,OB=1,∠AOB=90°,P(t,![]() t2﹣
t2﹣![]() t+3),
t+3),
∵点P和点D不能重合,
∴t≠7,
当1<t<7时,QA=t,QP=﹣![]() t2+
t2+![]() t,
t,
若△AOB与△AQP相似,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴t1=0(舍),t2=![]() 或t3=0(舍),t4=1(舍)
或t3=0(舍),t4=1(舍)
当t>7时,QA=t,PQ=![]() t2﹣
t2﹣![]() t,
t,
若△AOP与△AOB相似,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴t5=0(舍)或t=![]() 或t7=0(舍)t8=13,
或t7=0(舍)t8=13,
综上述,t=![]() 或
或![]() 或13.
或13.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0.53 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100B. 400C. 396D. 397