题目内容
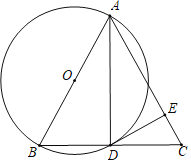
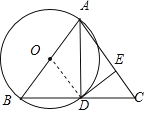
【题目】如图,△ABC中,AB=AC,AB是⊙O的直径,BC与⊙O交于点D,点E在AC上,且∠ADE=∠B.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求△ABC的面积.
【答案】(1)见解析;(2)S△ABC =40.
【解析】
(1)连接OD,证明OD⊥DE即可.因为AB是⊙O的直径,所以∠ADB=90°,因此∠B+∠BAD=90°.因为AO=DO,所以∠BAD=∠ADO.因为∠ADE=∠B,所以∠ADO+∠ADE=90°,即∠ODE=90°.可证DE是⊙O的切线;
(2)由AB=AC,∠ADB=90°可得点D是BC的中点,所以△ABC的面积是△ADC面积的2倍.因为点O是AB的中点,点D是BC的中点,可得AC=2DO=10,∠AED=180°-∠ODE=90°.因为CE=2,所以AE=8,根据射影定理DE2=AECE,所以DE=4,所以S△ABC=2S△ADC=2×(![]() ×ACDE)=40.
×ACDE)=40.
(1)连接OD,
∵AB是⊙O的直径
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵AO=DO,
∴∠BAD=∠ADO,
∵∠ADE=∠B,
∴∠ADO+∠ADE=∠BAD+∠B=90°,
即∠ODE=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)由(1)知,∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD是△ABC的中线,
∴点D是BC的中点,
又∵OB=OA,
∴DO是△ABC的中位线,
∵⊙O的半径为5,
∴AC=2DO=10,
∵CE=2,
∴AE=AC-CE=8,
∵DO是△ABC的中位线,
∴DO∥AC,
∴∠EDO+∠AED=180°,
∴∠AED=90°,
∴∠AED=∠DEC=90°,
∴∠EDC+∠C=90°,
∵ADC=180°-∠ADB=90°,
∴∠ADE+∠EDC=90°,
∴∠ADE=∠C,
∵∠AED=∠DEC,∠ADE=∠C,
∴△AED~△DEC,
∴![]() 即
即![]() ,
,
∴DE=4,
∴S△ADC=![]() ACDE=20,
ACDE=20,
∵AD是△ABC的中线,
∴S△ABC=2S△ADC=40.

 考前必练系列答案
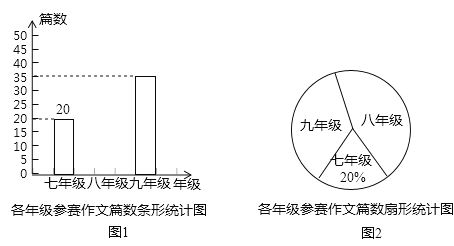
考前必练系列答案【题目】某学校为了了解九年级学生寒假的阅读情况,随机抽取了该年级的部分学生进行调查,统计了他们每人的阅读本数,设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)求扇形统计图中“优秀”类所在扇形的圆心角的度数;
(3)如果随机去掉一个数据,求众数发生变化的概率,并指出众数变化时,去掉的是哪个数据.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150721024/STEM/fd85c35161634f71b20809e4321f104b.png]
【题目】“凑够一拨人就走,管它红灯绿灯。”曾经有一段时间,“中国式过马路”现象引起社会广泛关注和热议.交通安全与我们的生活息息相关,“珍惜生命,文明出行”是每个公民应遵守的规则.某市为了了解市民对“闯红灯”的认识,随机调查了部分市民,并根据调查结果绘制了如下尚不完整的统计图表.(每位市民仅持一种观点)
调查结果统计表
观点 | 频数 |
A. 看到车少可以闯红灯 | 90 |
B. 无论什么时候都不能闯红灯 |
|
C. 因为车让行人,行人可以闯红灯 | 60 |
D. 凑够一拨人,大家一起过马路时可以闯红灯 |
|
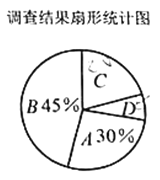
根据以上统计图表,解答下列问题:
(1)本次接受调查的市民共有_______人;![]() _______,
_______,![]() _______;
_______;
(2)扇形统计图中,扇形![]() 的圆心角度数是_______;
的圆心角度数是_______;
(3)若该市约有120万人,请估计“看到车少可以闯红灯”和“因为车让行人,行人可以闯红灯”观点的人数大约共有多少.