Question

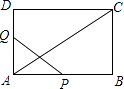
【题目】问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系，小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是　 　；

探索延伸：如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠EAF=∠BAD，上述结论是否仍然成立，并说明理由；

实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心(O处)北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以70海里/小时的速度前进，舰艇乙沿北偏东50°的方向以90海里/小时的速度，前进2小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．

Answer 1

【答案】问题背景：EF=BE+DF；探索延伸：仍然成立，理由见解析；实际应用：此时两舰艇之间的距离为320海里

【解析】

问题背景：延长FD到点G，使DG=BE，连接AG，证明△ABE≌△ADG，得到△AEF≌△AGF，证明EF=FG，得到答案；

探索延伸：连接EF，延长AE，BF相交于点C，利用全等三角形的性质证明EF=AE+FB．

实际应用：如图3，连接EF，延长AE，BF相交于点C，首先证明，∠FOE=∠AOB，利用结论EF=AE+BF求解即可．

解：问题背景：由题意：△ABE≌△ADG，△AEF≌△AGF，

∴BE=DG，EF=GF，

∴EF=FG=DF+DG=BE+FD．

故答案为：EF=BE+FD．

探索延伸：EF=BE+FD仍然成立．

理由：如图2，延长FD到点G，使DG=BE，连接AG

∵∠B+∠ADC=180°，∠ADG+∠ADC=180°，

∴∠B=∠ADG，

又∵AB=AD，

在△ABE和△ADG中，

，

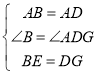∴△ABE≌△ADG(SAS)，

∴AE=AG，∠BAE=∠DAG，

又∵∠EAF=∠BAD，

∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD﹣∠EAF，

=∠BAD﹣∠BAD=∠BAD，

∴∠EAF=∠GAF．

在△AEF和△AGF中，

，

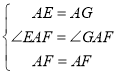∴△AEF≌△AGF(SAS)，

∴EF=FG，

又∵FG=DG+DF=BE+DF，

∴EF=BE+FD．

实际应用：如图3，连接EF，延长AE，BF相交于点C，

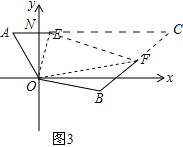
在四边形AOBC中，

∵∠AOB=30°+90°+20°=140°，∠FOE=70°=∠AOB，

又∵OA=OB，∠OAC+∠OBC=60°+120°=180°，符合探索延伸中的条件，

∴结论EF=AE+FB成立．

即，EF=AE+FB=2×(70+90)=320(海里)

答：此时两舰艇之间的距离为320海里．