题目内容
 如图,
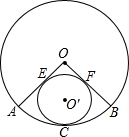
如图, 所对的圆心角∠AOB=60°,半径OA=R,求
所对的圆心角∠AOB=60°,半径OA=R,求 的长与内切圆⊙O′的周长的比.
的长与内切圆⊙O′的周长的比.
 解:如图,连接O'F,OO',并延长OO',
解:如图,连接O'F,OO',并延长OO',因为⊙O和⊙O′相切,所以OO′经过点C,
又因为OB与⊙O′相切于F,所以O'F⊥OB.
因为∠AOB=60°,所以∠BOC=30°,所以O'F=
 .
.设⊙O′的半径为r,所以r=
 =
= (R-r),所以R=3r,
(R-r),所以R=3r,所以
 的长与内切圆⊙O'的周长的比=1:2.
的长与内切圆⊙O'的周长的比=1:2.分析:利用弧长公式可求得弧AB的长,然后再利用圆相切求得小圆与大圆的半径关系,利用周长公式求比值.
点评:本题主要考查了切线性质和弧长公式,难度适中.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
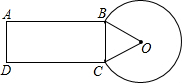 (1997•上海)如图,一种零件的横截面积是由矩形、三角形和扇形组成,矩形的长AB=2.45cm,扇形所在的圆的半径OB=1cm,扇形的弧所对的圆心角为300°,求这种零件的横截面的面积.(精确到0.01cm2,π≈3.142,
(1997•上海)如图,一种零件的横截面积是由矩形、三角形和扇形组成,矩形的长AB=2.45cm,扇形所在的圆的半径OB=1cm,扇形的弧所对的圆心角为300°,求这种零件的横截面的面积.(精确到0.01cm2,π≈3.142, 如图,等边三角形ABC内接于⊙O,则AC边所对的圆心角的度数为
如图,等边三角形ABC内接于⊙O,则AC边所对的圆心角的度数为 如图,弦AB所对的圆心角是60度,则弦AB所对的圆周角的度数为( )
如图,弦AB所对的圆心角是60度,则弦AB所对的圆周角的度数为( ) 如图,九(1)班同学要做一个展板,该展板的上沿是圆弧形,这条弧所在圆的半径为1.8m,所对的圆心角为100°,则弧长是
如图,九(1)班同学要做一个展板,该展板的上沿是圆弧形,这条弧所在圆的半径为1.8m,所对的圆心角为100°,则弧长是