题目内容
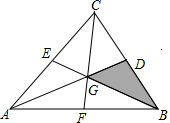如图：已知△ABC的三条中线AD=15、BE=12、CF=9，求△ABC的面积．
解：如图，把△BDG绕点D作中心对称变换成△CDM，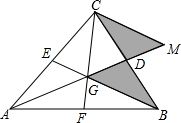
∴CG=
CF=6，CM=BG=BE=8，GM=2GD=AD=10，
∴△GCM是直角三角形，即∠GCM=90°，
∴S△GCM=
CG•CM=24，
∴S△BGC=S△GCM=24，
∴S△ABC=3S△BGC=72．
分析：如图，首先把△BDG绕点D作中心对称变换得到△CDM，然后根据重心的性质可以分别得到CG=CF=6，CM=BG=BE=8，GM=2GD=AD=10，由此利用勾股定理的逆定理可以证明△GCM是直角三角形，即∠GCM=90°，再利用三角形的面积公式求出S△GCM，最后可以得到S△BGC=S△GCM=24，而S△ABC=3S△BGC，由此即可求解．
点评：此题分别考查了旋转的性质、直角三角形的性质、勾股定理的逆定理及三角形的面积公式，其中对于中线问题一般可以尝试中心变换，此题把三条中线的有关线段集中在一起，构造出一个规则图形--直角三角形．
∴CG=
CF=6，CM=BG=BE=8，GM=2GD=AD=10，∴△GCM是直角三角形，即∠GCM=90°，
∴S△GCM=
CG•CM=24，∴S△BGC=S△GCM=24，
∴S△ABC=3S△BGC=72．
分析：如图，首先把△BDG绕点D作中心对称变换得到△CDM，然后根据重心的性质可以分别得到CG=
CF=6，CM=BG=BE=8，GM=2GD=AD=10，由此利用勾股定理的逆定理可以证明△GCM是直角三角形，即∠GCM=90°，再利用三角形的面积公式求出S△GCM，最后可以得到S△BGC=S△GCM=24，而S△ABC=3S△BGC，由此即可求解．点评：此题分别考查了旋转的性质、直角三角形的性质、勾股定理的逆定理及三角形的面积公式，其中对于中线问题一般可以尝试中心变换，此题把三条中线的有关线段集中在一起，构造出一个规则图形--直角三角形．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．