Question

【题目】请仔细阅读下面材料，然后解决问题：

在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”．例如： ， ；当分子的次数小于分母的次数时，我们称之为“真分式”，例如： ， ．我们知道，假分数可以化为带分数，例如： ，类似的，假分式也可以化为“带分式”（整式与真分式和的形式），例如： ．

（1）将分式化为带分式；

（2）当x取哪些整数值时，分式的值也是整数？

（3）当x的值变化时，分式的最大值为　　．

【答案】（1）2+；（2）x=0，2，﹣2，4；（3）.

【解析】试题分析：（1）仿照阅读材料中的方法加你个原式变形即可；

（2）原式变形后，根据结果为整数确定出整数x的值即可；

（3）原式变形后，确定出分式的最大值即可．

试题解析:（1）原式==2+；

（2）由（1）得： =2+，

要使为整数，则必为整数，

∴x﹣1为3的因数，

∴x﹣1=±1或±3，

解得：x=0，2，﹣2，4；

（3）原式==2+，

当x2=0时，原式取得最大值．

故答案为： .

【题型】解答题
【结束】
28

【题目】已知，△ABC中,AC＝BC,∠ACB＝90°，点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90°得线段BN，AN交直线BC于M．

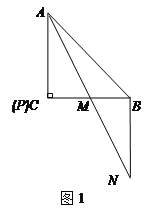
(1)图1，若点P与点C重合，则＝______,＝______．(直接写出结果)

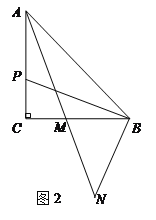
(2)图2，若点P在线段AC上，求证: AP＝2MC；

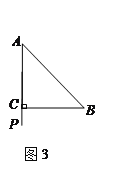
(3)图3，若点P在线段AC的延长线上，完成图形,并直接写出 ＝______．

Answer 1

【答案】⑴1, ; ⑵证明见解析; (3)

【解析】试题分析：（1）先求出 再利用“角角边”证明和 全等，根据全等三角形对应边相等可得 再求出 然后求解即可；
（2）过点作于，根据同角的余角相等求出，然后利用“角角边”证明和全等，根据全等三角形对应边相等可得 然后求出 再利用“角角边”证明和全等根据全等三角形对应边相等可得 整理即可得证；
（3）过点作交的延长线于，然后与（2）的求解方法相同．

试题解析：⑴1；

(2)证明：如图2，过点N作NE⊥BC于E，

∵线段PB绕点B逆时针旋转得线段BN，

∴∠PBC=∠BNE，

在△PBC和△BNE中,

∴BE=PC，NE=BC，

∴AP=ACPC=BCBE=CE，AC=NE，

在△ACM和△NEM中,

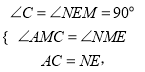
∴MC=ME，

∴CE=2MC，

∴AP=2MC；