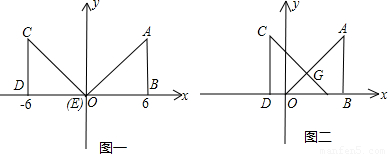题目内容
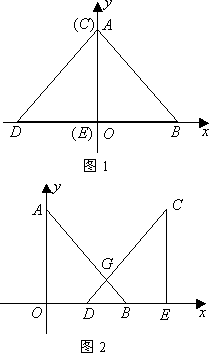
两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED按图1所示的位置放置A与C重合，O与E重合．
(1)求图1中，A，B，D三点的坐标．
(2)Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长的速度向右运动，当D点运动到与B点重合时停止，设运动x秒后Rt△CED和Rt△AOB重叠部分面积为y，求y与x之间的函数关系式．
(3)当Rt△CED以(2)中的速度和方向运动，运动时间x＝4秒时RT△CED运动到如图2所示的位置，求经过A，G，C三点的抛物线的解析式．
(4)现有一半径为2，圆心P在(3)中的抛物线上运动的动圆，试问⊙P在运动过程中是否存在⊙P与x轴或y轴相切的情况，若存在请求出P的坐标，若不存在请说明理由．
答案：
解析：
解析：
|
解：(1) (2)
当 当 可知： (求梯形 (3)图2中，作 (4)当 当 由 当 综上所述，符合条件的圆心 |
，
，
2分
时，位置如图A所示，作
，垂足为
，可知：
，
，
，
，
3分
时，位置如图B所示．
4分
的面积及
的面积时只要所用方法适当，所得结论正确均可给分)
与
的函数关系式为：
5分
，垂足为
，当
时，
，
，
可知：
，
，
6分
经过
三点的抛物线的解析式为：
7分
在运动过程中，存在
与坐标轴相切的情况，设
点坐标为
与
轴相切时，有
，
，由
得：
，
，得
，
与
轴相切时，有
，得：
，
有三个，其坐标分别是：
，
，
10分(每求出一个点坐标得1分)
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
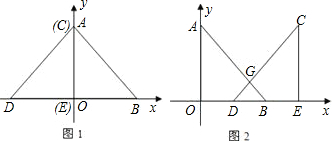程中是否存在⊙P与x轴或y轴相切的情况？若存在，请求出P的坐标，若不存在，请说明理由．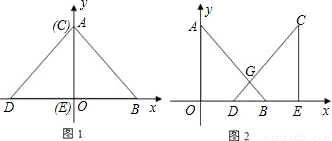
x2+bx+c过点A，G，求抛物线的解析式；
