题目内容
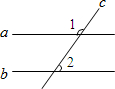如图，直线a、b被直线c所截，若a∥b，∠1=135°，则∠2等于
- A.45°
- B.30°
- C.60°
- D.75°
A
分析：由对顶角相等得出∠3的度数，再由a与b平行，利用两直线平行同旁内角互补得到∠3与∠2互补，即可求出∠2的度数．
解答：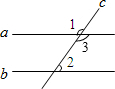
解：∵∠1与∠3为对顶角，
∴∠1=∠3=135°，
∵a∥b，
∴∠3+∠2=180°，
∴∠2=45°．
故选A
点评：此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．
分析：由对顶角相等得出∠3的度数，再由a与b平行，利用两直线平行同旁内角互补得到∠3与∠2互补，即可求出∠2的度数．
解答：
解：∵∠1与∠3为对顶角，∴∠1=∠3=135°，
∵a∥b，
∴∠3+∠2=180°，
∴∠2=45°．
故选A
点评：此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，是一个挂在墙壁上时钟的示意图．O是其秒针的转动中心，M是秒针的另一端，OM=8cm，l是过点O的铅直直线．现有一只蚂蚁P在秒针OM上爬行，蚂蚁P到点O的距离与M到l的距离始终相等．则1分钟的时间内，蚂蚁P被秒针OM携带的过程中移动的路程（非蚂蚁在秒针上爬行的路程）是
什么？
什么？
