题目内容
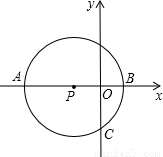
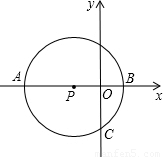
如图，已知点P在x轴上，⊙P与x轴相交于A、B两点，与y轴相交于点C，若B点坐标为（1，0），点C坐标为（0，﹣2）．
（1）求经过A、B、C三点的抛物线解析式；
（2）在所给的坐标系中画出抛物线的草图；
（3）观察图象，当x满足条件 _________ 时，y<0．
（1）求经过A、B、C三点的抛物线解析式；
（2）在所给的坐标系中画出抛物线的草图；
（3）观察图象，当x满足条件 _________ 时，y<0．
| 解：（1）连接AC、BC． ∵AB是⊙P的直径， ∴∠ACB=90°， 在Rt△ACB中，OC⊥AB，由射影定理得： OC2=OA·OB，即OA=OC2÷OB=4， ∴A（﹣4，0）． 设抛物线的解析式为：y=a（x+4）（x﹣1）， 依题意有：a（0+4）（0﹣1）=﹣2， 解得：a=  ．∴抛物线的解析式为：y=  （x+4）（x﹣1）= x2+ x﹣4；（2）如右图； （3）由图知：在A、B之间的抛物线图象都在x轴下方， 已知A（﹣4，0），B（1，0）， 故当﹣4<x<1时，y<0． |
 |
练习册系列答案
相关题目
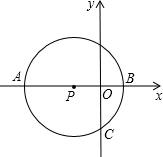如图，已知点P在x轴上，⊙P与x轴相交于A、B两点，与y轴相交于点C，若B点坐标为（1，0），点C坐标为（0，-2）．
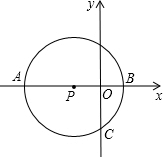如图，已知点P在x轴上，⊙P与x轴相交于A、B两点，与y轴相交于点C，若B点坐标为（1，0），点C坐标为（0，-2）．
