题目内容
如图所示,正方形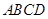 的面积为12,
的面积为12,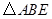 是等边三角形,点
是等边三角形,点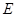 在正方形
在正方形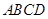 内,在对角线
内,在对角线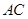 上有一点
上有一点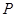 ,使
,使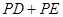 的和最小,则这个最小值为________
的和最小,则这个最小值为________
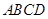 的面积为12,
的面积为12,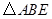 是等边三角形,点
是等边三角形,点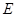 在正方形
在正方形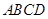 内,在对角线
内,在对角线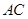 上有一点
上有一点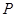 ,使
,使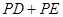 的和最小,则这个最小值为________
的和最小,则这个最小值为________

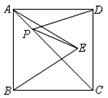
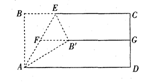
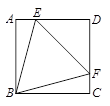
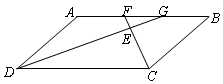
由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.
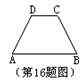
解:连接BD,与AC交于点F.

∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB= .
.
又∵△ABE是等边三角形,
∴BE=AB= .
.
故所求最小值为 .
.
故答案为: .
.
解:连接BD,与AC交于点F.

∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB=
 .
.又∵△ABE是等边三角形,
∴BE=AB=
 .
.故所求最小值为
 .
.故答案为:
 .
.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
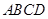 中,
中,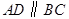 ,
,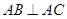 ,
,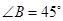 ,
,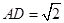 ,
,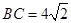 ,求
,求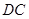 的长.
的长.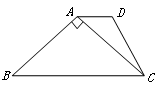
 为矩形纸片.把纸片
为矩形纸片.把纸片 恰好落在
恰好落在 边的中点
边的中点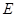 处,折痕为
处,折痕为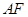 .若
.若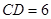 ,则
,则




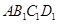 的边长为1,
的边长为1,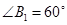 ;作
;作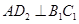 于点
于点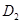 ,以
,以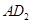 为一边,做第二个菱形
为一边,做第二个菱形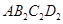 ,使
,使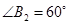 ;作
;作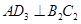 于点
于点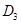 ,以
,以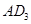 为一边做第三个菱形
为一边做第三个菱形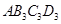 ,使
,使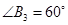 ;
; 依此类推,这样做的第
依此类推,这样做的第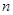 个菱形
个菱形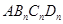 的边
的边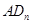 的长是 .
的长是 .
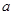 cm,其中矩形的长是宽的2倍,那么它们的面积
cm,其中矩形的长是宽的2倍,那么它们的面积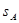 、
、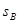 、
、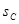 之间的关系式正确的是( ).
之间的关系式正确的是( ).