题目内容

已知：如图，在Rt△ABC中，点D₁是斜边AB的中点，过点D₁作D₁E₁⊥AC于点E₁，连接BE₁交CD₁于点D₂；过点D₂作D₂E₂⊥AC于点E₂，连接BE₂交CD₁于点D₃；过点D₃作D₃E₃⊥AC于点E₃，如此继续，可以依次得到点D₄、D₅、…、D_n，分别记△BD₁E₁、△BD₂E₂、△BD₃E₃、…、△BD_nE_n的面积为S₁、S₂、S₃、…S_n．设△ABC的面积是1，则S₁=________，S_n=________（用含n的代数式表示）．

$\text{[math]}$ $\text{[math]}$
分析：根据直角三角形的性质以及相似三角形的性质．再利用在△ACB中，D₂为其重心可得D₂E₁= $\text{[math]}$ BE₁，然后从中找出规律即可解答．
解答：易知D₁E₁∥BC，∴△BD₁E₁与△CD₁E₁同底同高，面积相等，以此类推；
∴S₁=S_△D1E1A= $\text{[math]}$ S_△ABC，
根据直角三角形的性质以及相似三角形的性质可知：D₁E₁= $\text{[math]}$ BC，CE₁= $\text{[math]}$ AC，S₁= $\text{[math]}$ S_△ABC；
∴在△ACB中，D₂为其重心，
又D₁E₁为三角形的中位线，∴D₁E₁∥BC，
∴△D₂D₁E₁∽△CD₂B，且相似比为1：2，
即 $\text{[math]}$ = $\text{[math]}$ ，
∴D₂E₁= $\text{[math]}$ BE₁，
∴D₂E₂= $\text{[math]}$ BC，CE₂= $\text{[math]}$ AC，S₂= $\text{[math]}$ S_△ABC，
∴D₃E₃= $\text{[math]}$ BC，CE₃= $\text{[math]}$ AC，S₃= $\text{[math]}$ S_△ABC…；
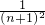∴S_n= $\text{[math]}$ S_△ABC．
故答案为： $\text{[math]}$ ， $\text{[math]}$ ．
点评：此题主要考查了相似三角形的判定与性质以及三角形中位线的性质和三角形的面积公式，解决本题的关键是据直角三角形的性质以及相似三角形的性质得到第一个三角形的面积与原三角形的面积的规律．