题目内容
已知:在△ABC中,AB=AC,∠B=30°,BC=6,点D在边BC上,点E在线段DC上,DE=3,△DEF是等边三角形,边DF、EF与边BA、CA分别相交于点M、N.求证:BD•CN=BM•CE.
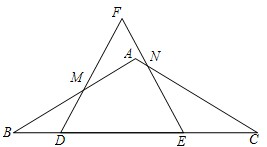
证明:∵△ABC中,AB=AC,
∴∠B=∠C.
∵△DEF是等边三角形,
∴∠FDE=∠FED.
∴∠MDB=∠AEC.
∴△BDM∽△CEN.
∴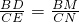 .
.
∴BD•CN=BM•CE.
分析:证明∠B=∠C,∠BDF=∠CEF,得出△BDM∽△CEN,根据相似三角形的性质得出结论.
点评:乘积的形式通常可以转化为比例的形式,通过相似三角形的性质得以证明.
∴∠B=∠C.
∵△DEF是等边三角形,
∴∠FDE=∠FED.
∴∠MDB=∠AEC.
∴△BDM∽△CEN.
∴
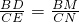 .
.∴BD•CN=BM•CE.
分析:证明∠B=∠C,∠BDF=∠CEF,得出△BDM∽△CEN,根据相似三角形的性质得出结论.
点评:乘积的形式通常可以转化为比例的形式,通过相似三角形的性质得以证明.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.