题目内容
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
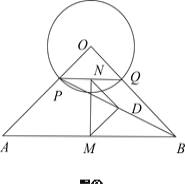
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
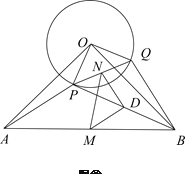
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.

(2)应用:
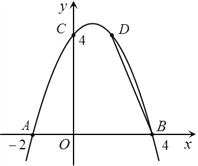
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.

【答案】(1)6;补图见解析,![]() (2)①见解析(答案不唯一)②见解析.
(2)①见解析(答案不唯一)②见解析.
【解析】
(1)如图1,根据线段中点的定义表示出EC和FC的长,则EF=EC+FC=![]() AB,得解;如图2,由EF=EC-FC=
AB,得解;如图2,由EF=EC-FC=![]() AB,得解;
AB,得解;
(2)①如图3,在CD上取一点M,使CM=CA,F为BM的中点,点E与点C重合;
②只要证明CF=20,点F在线段CD上即可.
解:(1)点![]() 在线段
在线段![]() 上时,
上时,
因为点E是线段AC的中点,所以CE=![]() AC,
AC,
因为点F是线段BC的中点,所以CF=![]() BC,
BC,
所以EF=CE+CF=![]() AC+
AC+![]() BC=
BC=![]() AB,
AB,
又AB=12,所以EF=6.
当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
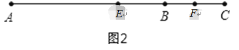
此时,EF=EC-FC═![]() AC-
AC-![]() BC=
BC=![]() AB.
AB.
答案为:6;EF=![]() AB.
AB.
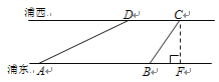
(2)①![]()
图3
如图,在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 与点
与点![]() 重合. (答案不唯一)
重合. (答案不唯一)
②因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
,
所以![]() .
.
因为![]() 米,所以
米,所以![]() 米.
米.
因为![]() 米,
米,![]() 米,
米,
所以![]() 米.
米.
因为点![]() 与点
与点![]() 重合,
重合,![]() 米,
米,
所以![]() 米,所以点
米,所以点![]() 落在线段
落在线段![]() 上.
上.
所以![]() 满足条件.
满足条件.

 名校课堂系列答案
名校课堂系列答案