题目内容
 如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点.若∠CDE=x°,∠ECD=y°,⊙B的半径为R,则
如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点.若∠CDE=x°,∠ECD=y°,⊙B的半径为R,则 的长度是
的长度是
- A.

- B.

- C.

- D.

B
分析:点C、D、E都在⊙P上,由圆周角定理可得:∠DPE=2y;然后在四边形BDPE中,求出∠B;最后利用弧长公式计算出结果.
解答: 解:根据题意,由切线长定理可知:PC=PD=PE,
解:根据题意,由切线长定理可知:PC=PD=PE,
即点C、D、E在以P为圆心,PC长为半径的⊙P上,
由圆周角定理得:∠DPE=2∠ECD=2y.
如图,连接BD、BE,则∠BDP=∠BEP=90°,
在四边形BDPE中,∠B+∠BDP+∠DPE+∠BEP=360°,
即:∠B+90°+2y+90°=360°,
解得:∠B=180°-2y.
∴ 的长度是:
的长度是: =
= .
.
故选B.
点评:本题考查圆的相关性质.解题关键是确定点C、D、E在⊙P上,从而由圆周角定理得到∠DPE=2∠ECD=2y.
分析:点C、D、E都在⊙P上,由圆周角定理可得:∠DPE=2y;然后在四边形BDPE中,求出∠B;最后利用弧长公式计算出结果.
解答:
 解:根据题意,由切线长定理可知:PC=PD=PE,
解:根据题意,由切线长定理可知:PC=PD=PE,即点C、D、E在以P为圆心,PC长为半径的⊙P上,
由圆周角定理得:∠DPE=2∠ECD=2y.
如图,连接BD、BE,则∠BDP=∠BEP=90°,
在四边形BDPE中,∠B+∠BDP+∠DPE+∠BEP=360°,
即:∠B+90°+2y+90°=360°,
解得:∠B=180°-2y.
∴
 的长度是:
的长度是: =
= .
.故选B.
点评:本题考查圆的相关性质.解题关键是确定点C、D、E在⊙P上,从而由圆周角定理得到∠DPE=2∠ECD=2y.

练习册系列答案
相关题目
 37、如图,⊙O1与⊙O2外切于点C,一条外公切线切两圆于点A,B,已知⊙O1的半径是9,⊙O2的半径是3,求∠BAC的度数.
37、如图,⊙O1与⊙O2外切于点C,一条外公切线切两圆于点A,B,已知⊙O1的半径是9,⊙O2的半径是3,求∠BAC的度数.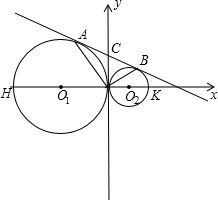 DNC是矩形?
DNC是矩形?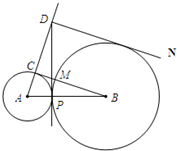 22、已知:如图,⊙A与⊙B外切于点P,BC切⊙A于点C,⊙A与⊙B的内公切线PD交AC于点D,交BC于点M.
22、已知:如图,⊙A与⊙B外切于点P,BC切⊙A于点C,⊙A与⊙B的内公切线PD交AC于点D,交BC于点M. (2012•淮安)如图,⊙M与⊙N外切,MN=10cm,若⊙M的半径为6cm,则⊙N的半径为
(2012•淮安)如图,⊙M与⊙N外切,MN=10cm,若⊙M的半径为6cm,则⊙N的半径为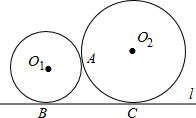 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.