题目内容
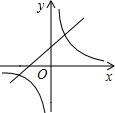
如图,在同一直角坐标系中,正比例函数y1=kx与反比例函数y2=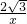 的图象分别
的图象分别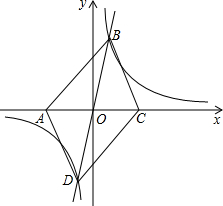 交于第一、第三象限的点B,D,已知点A(-a,0),C(a,0).
交于第一、第三象限的点B,D,已知点A(-a,0),C(a,0).
(1)直接判断并填写:四边形ABCD的形状一定是______;
(2)①当点B坐标为(p,2)时,四边形ABCD是矩形,试求p、k和a的值;
②直接写出不等式kx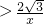 的解集;
的解集;
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标;若不能,说明理由.
解:(1)四边形ABCD的形状一定是平行四边形;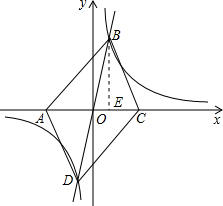
(2)①过B点作BE⊥x轴于E点,如图,
把B(p,2)代入y2=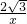 ,
,
∴p=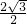 =
= ,
,
∴B点坐标为( ,2),
,2),
∴OB=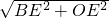 =
=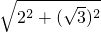 =
= ,
,
∵四边形ABCD是矩形,
∴OB=OC,
∴a= ,
,
把B( ,2)代入y1=kx得2=k
,2)代入y1=kx得2=k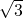 ,
,
解得k= ,
,
②点D与点B关于原点对称,点D的坐标为(- ,-2),
,-2),
等式kx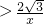 的解集为-
的解集为- <x<0或x>
<x<0或x> ;
;
(3)四边形ABCD不能是菱形.理由如下:
因为反比例函数图象与坐标轴没交点,即B点与点D不可能在y轴上,
所以BD与AC不可能垂直,
所以四边形ABCD不能是菱形.
分析:(1)由点A(-a,0),C(a,0)得OA=OC,再根据反比例函数图象关于原点中心对称,得到OB=OD,根据平行四边形的判定即可得到四边形ABCD为平行四边形;
(2)①过B点作BE⊥x轴于E点,把B(p,2)代入y2=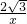 ,可求出p=
,可求出p= ,则B点坐标为(
,则B点坐标为( ,2),再利用勾股定理计算OB=
,2),再利用勾股定理计算OB=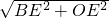 =
=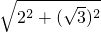 =
= ,再根据矩形的性质得
,再根据矩形的性质得
OB=OC,得到a= ,然后把B(
,然后把B( ,2)代入y1=kx可求出k的值;
,2)代入y1=kx可求出k的值;
②先得到反比例函数的性质得到点D的坐标为(- ,-2),然后观察图象得到当-
,-2),然后观察图象得到当- <x<0或x>
<x<0或x> 时,正比例函数y1=kx的图象都在反比例函数y2=
时,正比例函数y1=kx的图象都在反比例函数y2=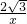 的图象的上方;
的图象的上方;
(3)由于比例函数图象与坐标轴没交点,即B点与点D不可能在y轴上,而点A、点C在x轴上,则BD与AC不可能垂直,根据菱形的判定方法得到四边形ABCD不能是菱形.
点评:本题考查了反比例函数综合题:反比例函数图象为双曲线,关于原点中心对称;点在图象上,点的坐标满足其解析式;掌握平行四边形、菱形的判定与性质和勾股定理.

(2)①过B点作BE⊥x轴于E点,如图,
把B(p,2)代入y2=
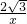 ,
,∴p=
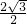 =
= ,
,∴B点坐标为(
 ,2),
,2),∴OB=
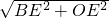 =
=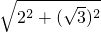 =
= ,
,∵四边形ABCD是矩形,
∴OB=OC,
∴a=
 ,
,把B(
 ,2)代入y1=kx得2=k
,2)代入y1=kx得2=k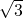 ,
,解得k=
 ,
,②点D与点B关于原点对称,点D的坐标为(-
 ,-2),
,-2),等式kx
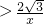 的解集为-
的解集为- <x<0或x>
<x<0或x> ;
;(3)四边形ABCD不能是菱形.理由如下:
因为反比例函数图象与坐标轴没交点,即B点与点D不可能在y轴上,
所以BD与AC不可能垂直,
所以四边形ABCD不能是菱形.
分析:(1)由点A(-a,0),C(a,0)得OA=OC,再根据反比例函数图象关于原点中心对称,得到OB=OD,根据平行四边形的判定即可得到四边形ABCD为平行四边形;
(2)①过B点作BE⊥x轴于E点,把B(p,2)代入y2=
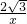 ,可求出p=
,可求出p= ,则B点坐标为(
,则B点坐标为( ,2),再利用勾股定理计算OB=
,2),再利用勾股定理计算OB=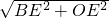 =
=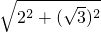 =
= ,再根据矩形的性质得
,再根据矩形的性质得OB=OC,得到a=
 ,然后把B(
,然后把B( ,2)代入y1=kx可求出k的值;
,2)代入y1=kx可求出k的值;②先得到反比例函数的性质得到点D的坐标为(-
 ,-2),然后观察图象得到当-
,-2),然后观察图象得到当- <x<0或x>
<x<0或x> 时,正比例函数y1=kx的图象都在反比例函数y2=
时,正比例函数y1=kx的图象都在反比例函数y2=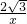 的图象的上方;
的图象的上方;(3)由于比例函数图象与坐标轴没交点,即B点与点D不可能在y轴上,而点A、点C在x轴上,则BD与AC不可能垂直,根据菱形的判定方法得到四边形ABCD不能是菱形.
点评:本题考查了反比例函数综合题:反比例函数图象为双曲线,关于原点中心对称;点在图象上,点的坐标满足其解析式;掌握平行四边形、菱形的判定与性质和勾股定理.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
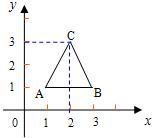 20、如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).
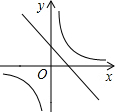
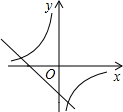
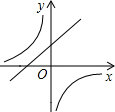
20、如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).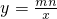 和y=mx+m(m≠0,n≠0)的图象正确的是
和y=mx+m(m≠0,n≠0)的图象正确的是



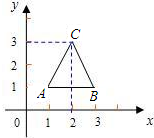 如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).
如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).