题目内容
【题目】如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为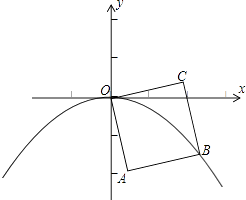
【答案】﹣ ![]()
【解析】解:如图,连接OB,
∵四边形OABC是边长为1的正方形,
∴∠BOC=45°,OB=1× ![]() =
= ![]() ,
,
过点B作BD⊥x轴于D,
∵OC与x轴正半轴的夹角为15°,
∴∠BOD=45°﹣15°=30°,
∴BD= ![]() OB=
OB= ![]() ,
,
OD= ![]() =
= ![]() ,
,
∴点B的坐标为( ![]() ,﹣
,﹣ ![]() ),
),
∵点B在抛物线y=ax2(a<0)的图象上,
∴a( ![]() )2=﹣
)2=﹣ ![]() ,
,
解得a=﹣ ![]() .
.
所以答案是:﹣ ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目