题目内容
 如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知AD=BC,AD⊥CB.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知AD=BC,AD⊥CB.(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
考点:圆心角、弧、弦的关系,勾股定理,正方形的判定与性质
专题:
分析:(1)欲证明AB=CD,只需证得
=
;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
 |
| AB |
 |
| CD |
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
解答: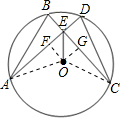 (1)证明:如图,∵AD=BC,
(1)证明:如图,∵AD=BC,
∴
=
,
∴
-
=
-
,即
=
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
 (1)证明:如图,∵AD=BC,
(1)证明:如图,∵AD=BC,∴
 |
| AD |
 |
| BC |
∴
 |
| AD |
 |
| BD |
 |
| BC |
 |
| BD |
 |
| AB |
 |
| CD |
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
|
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
点评:本题考查了勾股定理,正方形的判定与性质,垂径定理以及圆周角、弧、弦间的关系.注意(2)中辅助线的作法.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
抛物线y=x2-2x-3与y轴交于A点,则点A的坐标是( )
| A、(-1,0) |
| B、(0,-3) |
| C、(0,3) |
| D、(3,0) |
 如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE. 如图,∠BOD的度数是
如图,∠BOD的度数是