题目内容
 如图,在△ABC中,∠C=90°,∠A=45°,D为AC上一点,∠BDC=60°,AD=2,求BC.
如图,在△ABC中,∠C=90°,∠A=45°,D为AC上一点,∠BDC=60°,AD=2,求BC.考点:等腰直角三角形,含30度角的直角三角形,勾股定理
专题:
分析:设BC=x,则AC=x,CD=x-2,在Rt△BCD中,∠BDC=60°,可得
=tan60°=
,代入可求得x的值,即可求出BC的长.
| BC |
| CD |
| 3 |
解答:解:
∵∠C=90°,∠A=45°,
∴可设BC=AC=x,
∵AD=2,
∴CD=x-2,
在Rt△BCD中,tan∠BDC=
,
∴
=
,解得x=3+
,
即BC=3+
.
∵∠C=90°,∠A=45°,
∴可设BC=AC=x,
∵AD=2,
∴CD=x-2,
在Rt△BCD中,tan∠BDC=
| BC |
| CD |
∴
| x |
| x-2 |
| 3 |
| 3 |
即BC=3+
| 3 |
点评:本题主要考查等腰三角形的性质及含特殊角的直角三角形的性质,利用三角函数的定义找到BC和CD之间的关系是解题的关键,注意方程思想的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 如图,四边形ABEG、GEFH、HFCD都是正方形,请你在图中找出一对相似比不等于1的相似三角形,并说明理由.
如图,四边形ABEG、GEFH、HFCD都是正方形,请你在图中找出一对相似比不等于1的相似三角形,并说明理由.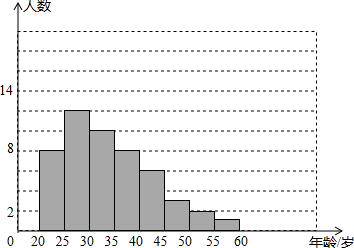
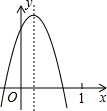 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: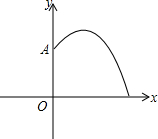 如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25
如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25