题目内容
【题目】如图所示,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.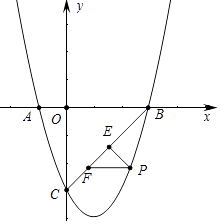
(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点P,过点p作PE⊥BC于点E,作PF平行于x轴交直线BC于点F,求△PEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由.
【答案】
(1)解:把A(﹣1,0),B(3,0)两点坐标代入抛物线y=ax2+bx﹣3,
得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)解:如图1中,连接PB、PC.设P(m,m2﹣2m﹣3),

∵B(3,0),C(0,﹣3),
∴OB=OC,
∴∠OBC=45°,
∵PF∥OB,
∴∠PFE=∠OBC=45°,
∵PE⊥BC,
∴∠PEF=90°,
∴△PEF是等腰直角三角形,
∴PE最大时,△PEF的面积中点,此时△PBC的面积最大,
则有S△PBC=S△POB+S△POC﹣S△BOC= ![]() 3(﹣m2+2m+3)+
3(﹣m2+2m+3)+ ![]() 3m﹣
3m﹣ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴m= ![]() 时,△PBC的面积最大,此时△PEF的面积也最大,
时,△PBC的面积最大,此时△PEF的面积也最大,
此时P( ![]() ,﹣
,﹣ ![]() ),
),
∵直线BC的解析式为y=x﹣3,
∴F(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴PF= ![]() ,
,
∵△PEF是等腰直角三角形,
∴EF=EP= ![]() ,
,
∴C△PEF最大值= ![]() +
+ ![]() .
.
(3)解:①如图2中,

当N与C重合时,点N关于对称轴的对称点P,此时思想MNQP是正方形,易知P(2,﹣3).点P横坐标为2,
②如图3中,当四边形PMQN是正方形时,作PF⊥y轴于N,ME∥x轴,PE∥y轴.

易知△PFN≌△PEM,
∴PF=PE,设P(m,m2﹣2m﹣3),
∵M(1,﹣4),
∴m=m2﹣2m﹣3﹣(﹣4),
∴m= ![]() 或
或 ![]() (舍弃),
(舍弃),
∴P点横坐标为 ![]()
所以满足条件的点P的横坐标为2或 ![]() .
.
【解析】分析:(1)把A,B两点坐标代入抛物线,即可求出此函数解析式。
(2)由B(3,0),C(0,﹣3)两点坐标,可得出△OBC是等腰直角三角形,根据已知PE⊥BC,PF∥x轴,可证得△PEF是等腰直角三角形,则PE最大时,△PEF的面积中点,此时△PBC的面积最大,求出S△PBC与m的函数关系式,求出其顶点坐标,即可得到△PBC的面积最大时m的值,再求出直线BC的解析式,即可求得点F的坐标,求出PF、EF、EP的长,即可△PEF周长的最大值。
(3)①当N与C重合时,点N关于对称轴的对称点P,此时思想MNQP是正方形,易知P点坐标;②当四边形PMQN是正方形时,作PF⊥y轴于N,ME∥x轴,PE∥y轴.易知△PFN≌△PEM,得到F=PE,建立方程,求解即可得到满足条件的点P的横坐标。
【考点精析】本题主要考查了二次函数的最值和轴对称的性质的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布直方图和频数、频率分布表.请你根据图表提供的信息,解答下列问题:
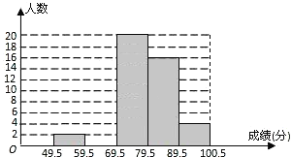
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 |
| 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
(1)频数、频率分布表中![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少?