题目内容
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边中点,点E是BC边上一点,将△ADE沿DE折叠,得到△FDE,使△FDE与△BDE重叠部分的面积是△AEB面积的![]() ,若AC=3,BC=6,则线段BE的长为__________.
,若AC=3,BC=6,则线段BE的长为__________.

【答案】![]()
【解析】
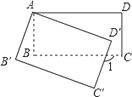
分两种情形:①设AB交EF于O,当DO=![]() AB,即O点为BD的中点时,△FDE与△BDE重叠部分的面积是△AEB面积的
AB,即O点为BD的中点时,△FDE与△BDE重叠部分的面积是△AEB面积的![]() ;②当DF平分线段BE时,满足条件,分别求解即可解决问题.
;②当DF平分线段BE时,满足条件,分别求解即可解决问题.
①如图1,设AB交EF于O,当DO=![]() AB,即O点为BD的中点时,△FDE与△BDE重叠部分的面积是△AEB面积的
AB,即O点为BD的中点时,△FDE与△BDE重叠部分的面积是△AEB面积的![]() ,
,

作DM⊥AE于点M,DN⊥FE于点N,连接FB,
∵AC=3,BC=6,∠C=90°,
∴AB=![]() ,
,
∵D是AB边的中点,
∴AD=BD=![]() ,S△ADE=S△BDE,
,S△ADE=S△BDE,
∵∠AED=∠FED,
∴在△DME与△DNE中
∴△DME≌△DNE,
∴DM=DN,
∵
∴![]() ,即AE=2OE,
,即AE=2OE,
∵AE=FE,
∴OE=OF,
∵OD=OB,
∴四边形DFBE为平行四边形,
∴FD=AD=BE=![]() ;
;
②如图2,当DF平分线段BE时,满足条件,

∵BD=AD,OE=OB,
∴AE∥OD,
∴∠AED=∠EDO=∠ADE,
∴AE=AD=![]() ,
,
在△ACE中,CE= ,
,
∴BE=BC-CE=6-![]() =
=![]() ,
,
综上BE的值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目