��Ŀ����
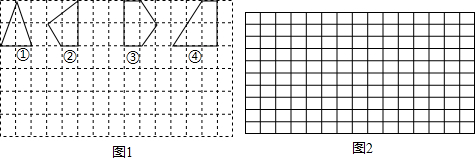
��ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ��㣬�и�㣬�Ը��Ϊ����Ķ���νи�����Σ��������ε����ΪS���������ϸ��ĸ�����Ϊx��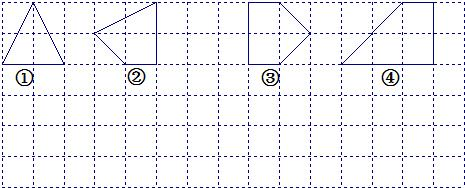
��1����ͼ�еĸ�����Σ����ڲ���ֻ��һ����㣬���ǵ����������ϸ��ĸ����͵Ķ�Ӧ��ϵ���±�����д��S��x֮��Ĺ�ϵʽ��
��S=
| ������� | �� | �� | �� | �� | �� |
| �������S | 2 | 2.5 | 3 | 4 | �� |
| �����ϸ��ĸ�����x | 4 | 5 | 6 | 8 | �� |
��3���������̽��������������ڲ�����ֻ��n�����ʱ������S��x�������Ĺ�ϵ��
��S=
��������1���ɣ�1������ֱ�ӵõ�S=
x��
��2����ͼ��֪������ڲ����ж���ֻ��2���ʱ���ٵĸ����ϸ��ĸ���Ϊ10�����Ϊ6���ڵĸ����ϸ��ĸ���Ϊ4�����Ϊ3���۵ĸ����ϸ��ĸ���Ϊ6�����Ϊ4��S=
x+1��
��3����ͼ��֪������ڲ����ж���ֻ��n���ʱ�����Ϊ��S=
+��n-1����
| 1 |
| 2 |
��2����ͼ��֪������ڲ����ж���ֻ��2���ʱ���ٵĸ����ϸ��ĸ���Ϊ10�����Ϊ6���ڵĸ����ϸ��ĸ���Ϊ4�����Ϊ3���۵ĸ����ϸ��ĸ���Ϊ6�����Ϊ4��S=
| 1 |
| 2 |
��3����ͼ��֪������ڲ����ж���ֻ��n���ʱ�����Ϊ��S=
| x |
| 2 |
����⣺

��1��S=
x��
��2��S=
x+1��
��3��S=
+n-1��

��1��S=
| 1 |
| 2 |
��2��S=
| 1 |
| 2 |
��3��S=
| x |
| 2 |
������������Ҫ����ͼ�б�����Լ�����õ����ݣ��ܽ�����ɣ�Ѱ�ҹ�����һ���Ƚ����ѵĻ����Ҫ��ϸ�۲�ʹ��������㣮

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
 31����ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ��㣬�и�㣮���۲�ͼ��ÿһ�������Σ�ʵ�ߣ��������ϵĸ��ĸ�������ش��������⣺
31����ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ��߳�Ϊ1��С�����θ��ӣ�С�����εĶ��㣬�и�㣮���۲�ͼ��ÿһ�������Σ�ʵ�ߣ��������ϵĸ��ĸ�������ش��������⣺