题目内容
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+ kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
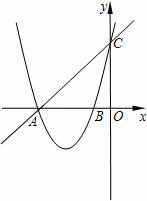
解:(1)由x=0得y=0+4=4,则点C的坐标为(0,4);
由y=0得x+4=0,解得x=﹣4,则点A的坐标为(﹣4,0);
把点C(0,4)代入y=x2+kx+k﹣1,得k﹣1=4,
解得:k=5,
∴此抛物线的解析式为y=x2+5x+4,
∴此抛物线的对称轴为x=﹣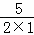 =﹣
=﹣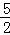 .
.
令y=0得x2+5x+4=0,
解得:x1=﹣1,x2=﹣4,
∴点B的坐标为(﹣1,0).
(2)∵A(﹣4,0),C(0,4),
∴OA=OC=4,
∴∠OCA=∠OAC.
∵∠AOC=90°,OB=1,OC=OA=4,
∴AC=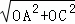 =4
=4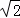 ,AB=OA﹣OB=4﹣1=3.
,AB=OA﹣OB=4﹣1=3.
∵点D在y轴负半轴上,∴∠ADC<∠AOC,即∠ADC<90°.
又∵∠ABC>∠BOC,即∠ABC>90°,∴∠ABC>∠ADC.
∴由条件“以A、C、D为顶点的三角形与△ABC相似”可得△CAD∽△ABC,
∴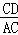 =
=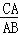 ,即
,即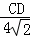 =
=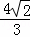 ,
,
解得:CD=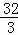 ,
,
∴OD=CD﹣CO=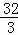 ﹣4=
﹣4=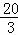 ,
,
∴点D的坐标为(0,﹣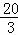 ).
).
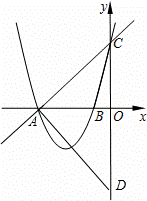

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

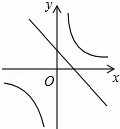
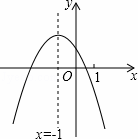
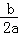 与反比例函数y=
与反比例函数y=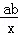 在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )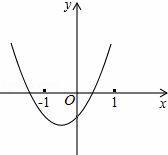
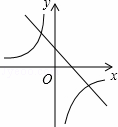 B.
B.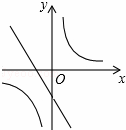 C.
C.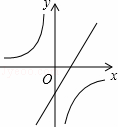 D.
D.