题目内容
关于x的一元二次方程（k+1）x2+2x-1=0有两个不相等的实数根，则k的取值范围为 ．
考点：根的判别式,一元二次方程的定义
专题：
分析：根据关于x的一元二次方程（k+1）x2+2x-1=0有两个不相等的实数根，可得出判别式大于0，再求得k的取值范围．
解答：解：∵关于x的一元二次方程（k+1）x2+2x-1=0有两个不相等的实数根，
∴△=4+4（k+1）＞0，
解得k＞-
，
∵k+1≠0，
∴k≠-1，
∴k的取值范围k＞-
且k≠-1，
故答案为k＞-
且k≠-1．
∴△=4+4（k+1）＞0，
解得k＞-
| 5 |
| 4 |
∵k+1≠0，
∴k≠-1，
∴k的取值范围k＞-
| 5 |
| 4 |
故答案为k＞-
| 5 |
| 4 |
点评：本题考查了根的判别式，总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图1，将在Rt△ABC绕其锐角顶点A旋转90°得到Rt△ADE，连接BE，延长DE、BC相交于点F，则有∠BFE=90°，且四边形ACFD是一个正方形．
如图，在△ABC中，AB=7cm，AC=4cm，AD为中线，则△ABD与△ACD的周长之差=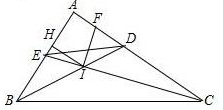
如图，△ABC中，∠A=90°，角平分线BD、CE交于点I，IF⊥CE交CA于F，IH⊥AB于H，下列结论：①∠DIF=45°；②CF+BE=BC；③AE+AF=2AH；④S四边形BEDC=2S△IBC，其中正确的结论为