Question

如图①，在平面直角坐标系中，将n个边长为1的正方形并排组成矩形OABC，相邻两边OA和OC分别落在x轴和y轴的正半轴上．现将矩形OABC绕点O顺时针旋转，使得点B落到x轴的正半轴上（如图②），设抛物线y=ax²+bx+c（a＜0），如果抛物线同时经过点O，B，C．
（1）当n=4时，a=

 

；
（2）a关于n的关系式是

 

．

Answer 1

考点：二次函数综合题

专题：

分析：（1）当n=4时，OC=1，BC=4，设所求抛物线解析式为y=ax²+bx，过C作CD⊥OB于点D，则Rt△OCD∽Rt△CBD，得出OD：CD=OC：BC=1：4，设OD=t，则CD=4t，根据勾股定理OD²+CD²=OC²，求出t，得出C的坐标，把B、C坐标代入抛物线解析式即可得到方程组，求出a即可；
（2）根据a=2、3和（1）总结规律，可以得到答案．

解答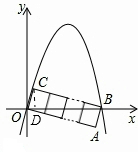：解：（1）如图当n=4时，OC=1，BC=4，
设所求抛物线解析式为y=ax²+bx，
过C作CD⊥OB于点D，
则Rt△OCD∽Rt△OBC，
∴

OD

CD

=

OC

BC

=

1

4

，
设OD=t，则CD=4t，
∵OD²+CD²=OC²，
∴（4t）²+t²=1²，
∴t=

17

17

，
∴C（

17

17

，

4 17

17

），
又∵B（

17

，0），
∴把B、C坐标代入抛物线解析式，得

0=17a+ 17 b 4 17 17 = 1 17 a+ 17 17 b

，
解得：a=-

17

4

；

（2）当n=2时，OC=1，BC=2，
∴OB=

5

，
∴1×2=

5

CD，B（

5

，0）
∴CD=

2 5

5

，
∴OD=

5

5

，
∴C（

5

5

，

2 5

5

）
设所求抛物线解析式为y=ax²+bx，
∴

0=5a+ 5 b 2 5 5 = 1 5 a+ 5 5 b

，
解得：a=-

5

2

；
同理当n=3时，a=-

10

3

；
∴可以得出a关于n的关系式是：a=-

n2+1

n

．
故答案为：（1）-

17

4

，（2）a=-

n2+1

n

．

点评：本题主要考查相似三角形的性质和判定，正方形的性质，用待定系数法求二次函数的解析式，解二元一次方程组，勾股定理等知识点的理解和掌握．此题难度较大，注意掌握数形结合思想与方程思想的应用．