题目内容

若2x2-5x+2＜0，则
4x2-4x+1
+2|x-2|=
 
．
考点：一元二次不等式
专题：
分析：解出不等式求出x的取值范围，然后开方、去绝对值后解答．
解答：解：先解不等式：2x2-5x+2＜0，
因式分解，得（x-2）（2x-1）＜0，
即
x-2＞0
2x-1＜0
或
x-2＜0
2x-1＞0
，
无解或
1
2
＜x＜2．
综上，
1
2
＜x＜2，
可得
4x2-4x+1
+2|x-2|
=
(2x-1)2
+2|x-2|
=2x-1+2（2-x）
=2x-1+4-2x
=3．
故答案为3．
点评：本题考查了一元二次不等式，熟悉不等式的解法和平方根、绝对值的运算是解题的关键．
练习册系列答案
相关题目
已知M=
9+4m
+
25-2m
+
169m+1
-
-m2
，试判断M的值是否确定？如果确定，请求出M的值；如果不确定，请说出理由．
m+0﹦
 
；-m+m﹦
 
．
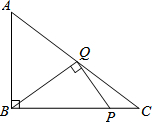如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，P是BC边上的动点．设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是
 
．
计算：[-（-2）2]3=
 
；-（y4）•（-y）5=
 
．
1，-8，-0.23，
1
3
，0，1
2
3
，-
2
3
，300%中是整数的有
 
．
若a-b=4，ab=-2，则2a2b-2ab2的值是（　　）
A、8B、16C、-8D、-16
方程x（x-5）=0的根是（　　）
A、x=0
B、x=5
C、x1=0，x2=5
D、x1=0，x2=-5
计算：
6
+4
3
+3
2
(
6
+
3
)(
3
+
2
)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网