题目内容
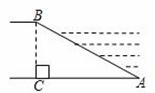
在Rt△ABC中,∠ACB=90°,现将Rt△ABC绕点C逆时针旋转90°,得到Rt△DEC(如图①)
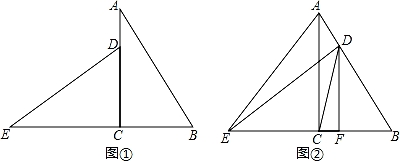
(1)请判断ED与AB的位置关系,并说明理由.
(2)如图②,将Rt△DEC沿CB方向向右平移,且使点D恰好落在AB边上,记平移后的三角形为Rt△DEF,连接AE、DC,求证:∠ACD=∠AED.
【考点】旋转的性质;平移的性质.
【专题】证明题.
【分析】(1)延长ED交AB于F,如图①,根据旋转的性质得∠A=∠E,再利用∠A+∠B=90°得到∠E+∠B=90°,则根据三角形内角和定理易得∠EFB=90°,于是利用垂直的定义可判断ED⊥AB;
(2)如图②,先利用平移的性质和(1)中的结论得到DE⊥AB,即∠ADE=90°,则利用圆周角定理的推论得到点C和点D在以AE为直径的圆上,然后根据圆周角定理即可得到结论.
【解答】(1)解:ED⊥AB.理由如下:
延长ED交AB于F,如图①,
∵Rt△ABC绕点C逆时针旋转90°,得到Rt△DEC,
∴∠A=∠E,
∵∠A+∠B=90°
∴∠E+∠B=90°
∴∠EFB=90°
∴ED⊥AB;
(2)证明:如图②,
∵将Rt△DEC沿CB方向向右平移,且使点D恰好落在AB边上,
∴DE⊥AB,
∴∠ADE=90°,
∵∠ACE=90°,
∴点C和点D在以AE为直径的圆上,
∴∠ACD=∠AED.


【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决(2)的关键是确定点C和点D在以AE为直径的圆上,从而利用圆周角定理求解.

练习册系列答案
相关题目
 ﹣3=
﹣3= .
. ),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )

 ,则AC的长是( ).
,则AC的长是( ).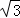 米 B.10米
米 B.10米