题目内容
在 、π、
、π、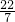 、
、 、3.14、0、
、3.14、0、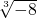 、0.
、0. 、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有
、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有
- A.2个
- B.3个
- C.4个
- D.5个
B
分析:先根据立方根、平方根的定义进行计算,再根据无理数的定义:无理数就是无限不循环小数,对每一个实数进行分析,找出其中的无理数即可.
解答:∵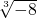 =-3,
=-3, =-3,
=-3,
∴在 、π、
、π、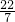 、
、 、3.14、0、
、3.14、0、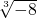 、0.
、0. 、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有π、
、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有π、 、0.1010010001…(每两个相邻的1之间依次多一个0),共3个,
、0.1010010001…(每两个相邻的1之间依次多一个0),共3个,
故选B.
点评:本题主要考查了无理数的定义,无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.
分析:先根据立方根、平方根的定义进行计算,再根据无理数的定义:无理数就是无限不循环小数,对每一个实数进行分析,找出其中的无理数即可.
解答:∵
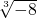 =-3,
=-3, =-3,
=-3,∴在
 、π、
、π、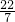 、
、 、3.14、0、
、3.14、0、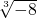 、0.
、0. 、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有π、
、0.1010010001…(每两个相邻的1之间依次多一个0)这9个实数中,无理数有π、 、0.1010010001…(每两个相邻的1之间依次多一个0),共3个,
、0.1010010001…(每两个相邻的1之间依次多一个0),共3个,故选B.
点评:本题主要考查了无理数的定义,无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 5个城市的国标标准时间(单位:时)在数轴上的表示(例如:伦敦时间的0点是汉城时间的9点)如图所示,为了庆祝中国人民解放军海军成立60周年,海上大阅兵在2009年4月23日14时20分在青岛附近黄海海域举行,请问北京时间2009年4月23日14时应是( )
5个城市的国标标准时间(单位:时)在数轴上的表示(例如:伦敦时间的0点是汉城时间的9点)如图所示,为了庆祝中国人民解放军海军成立60周年,海上大阅兵在2009年4月23日14时20分在青岛附近黄海海域举行,请问北京时间2009年4月23日14时应是( )