题目内容
 甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:(1)最先到达终点的是
(2)在比赛过程中,乙队在
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
分析:(1)根据两函数的图象即可得出结论;
(2)根据乙的函数的倾斜程度的变化,可得出乙在1和3分钟时两次加速;
(3)如果第一次加速后保持这个速度,求甲乙两队能否到达,就是求AB段的函数过不过(5,800).可用待定系数法求出AB段的函数关系式,然后进行判断即可.
(2)根据乙的函数的倾斜程度的变化,可得出乙在1和3分钟时两次加速;
(3)如果第一次加速后保持这个速度,求甲乙两队能否到达,就是求AB段的函数过不过(5,800).可用待定系数法求出AB段的函数关系式,然后进行判断即可.
解答:解:(1)根据图象可以得到最先到达终点的是乙,
比乙队领先5-4.4=0.6分钟;
(2)根据图象知道在第1分钟和第3分钟时两次加速;
(3)设AB所在直线的解析式为y=kx+b,
则
∴
∴y=175x-75,
当y=800米时,800=175x-75,
∴x=5,
∴甲、乙两队同时到达终点.
比乙队领先5-4.4=0.6分钟;
(2)根据图象知道在第1分钟和第3分钟时两次加速;
(3)设AB所在直线的解析式为y=kx+b,
则
|
|
当y=800米时,800=175x-75,
∴x=5,
∴甲、乙两队同时到达终点.
点评:此题读懂图象是关键,然后借助函数图象表达题目中的信息解决问题,解题要注意题中分段函数的意义.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
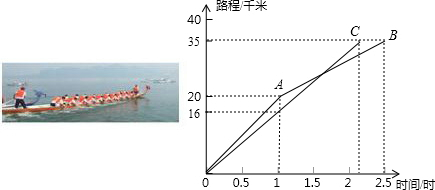

 某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题: