��Ŀ����
����Ŀ��������y����x2+x+b��x�ύ��A��B���㣬��y�ύ�ڵ�C��
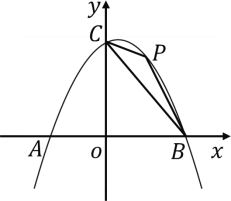
��1����B��������2��0��
����ʵ��b��ֵ��
����ͼ1����E���������ڵ�һ�����ڵ�ͼ���ϵĵ㣬���CBE��������ֵ����ʱ��E�����꣮
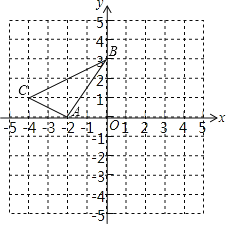
��2����ͼ2�������ߵĶԳ��ύx���ڵ�D�����������ϴ��ڵ�P��ʹ��P��B��C��D�ĵ��ܹ���ƽ���ı��Σ���ʵ��b��ֵ������ʾ������M��N������ΪM��x��y����N��x��y�������߶�MN���е�����Ϊ��![]() ��
��![]() ��
��

���𰸡���1����b��2���ڡ�CBE��������ֵΪ1����ʱE��1��2������2��b����1+![]() ��b��
��b��![]() ����
����![]() ��
��![]() ��
��
��������
��1��������B��2��0������y����x2+x+b������b��
����E��m����m2+m+2�������BC��ֱ�߽���ʽΪy����x+2������E��BC��ֱ��ֱ�߽���ʽΪy��x��m2+2�������ֱ�߽���F����EF���ʱ����CBE��������
��2������C��0��b����B��![]() ��0������M��t����t2+t+b�������öԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�������������⣺����CM��BDΪƽ���ı��εĶԽ���ʱ��
��0������M��t����t2+t+b�������öԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�������������⣺����CM��BDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��0�����b����1+
��0�����b����1+![]() ������BM��CDΪƽ���ı��εĶԽ���ʱ��
������BM��CDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��
��![]() ��b�⣻����BC��MDΪƽ���ı��εĶԽ���ʱ��
��b�⣻����BC��MDΪƽ���ı��εĶԽ���ʱ��![]() ��
��![]() ��
��![]() ��
��![]() �����b��
�����b��![]() ��b����
��b����![]() ���ᣩ��
���ᣩ��
�⣺��1��������B��2��0������y����x2+x+b��
�õ�0����4+2+b��
��b��2��
��C��0��2����B��2��0����
��BC��ֱ�߽���ʽΪy����x+2��
��E��m����m2+m+2����
����E��BC��ֱ��ֱ�߽���ʽΪy��x��m2+2��
��ֱ��BC���䴹�ߵĽ���ΪF��![]() ����
����![]() +2����
+2����
��EF��![]() ����
����![]() +2����
+2����![]() [��
[��![]() ��m��1��2+
��m��1��2+![]() ]��
]��
��m��1ʱ��EF�����ֵ![]() ��
��
��S��![]() ��BC��EF��
��BC��EF��![]() ��2
��2![]() ��
��![]() ��1��
��1��
���CBE��������ֵΪ1����ʱE��1��2����
��2���������ߵĶԳ���Ϊx��![]() ��
��
��D��![]() ��0����
��0����
��������x�����������㣬
�����1+4b��0��
��b����![]() ��
��
��C��0��b����B��![]() ��0����
��0����
��M��t����t2+t+b����
����CM��BDΪƽ���ı��εĶԽ���ʱ��
C��M���е�Ϊ��![]() ��
��![]() ����B��D���е�Ϊ��
����B��D���е�Ϊ��![]() ��0����
��0����
��![]() ��
��![]() ��
��![]() ��0��
��0��
��ã�b����1+![]() ��b����1��
��b����1��![]() ����ȥ����
����ȥ����
��b����1+![]() ��
��
����BM��CDΪƽ���ı��εĶԽ���ʱ��
B��M���е�Ϊ��![]() ��
��![]() ����C��D���е�Ϊ��
����C��D���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��b�⣻
����BC��MDΪƽ���ı��εĶԽ���ʱ��
B��C���е�Ϊ��![]() ��
��![]() ����M��D���е�Ϊ��
����M��D���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��ã�b��![]() ��b����
��b����![]() ���ᣩ��
���ᣩ��
����������b����1+![]() ��b��
��b��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�