Question

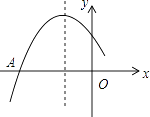
【题目】如图1，在平面直角坐标系中，，且满足式子.

（1）求出的值；

（2）①在轴的正半轴上存在一点，使的面积等于的面积的一半，求出点的坐标；

②在坐标轴的其它位置是否存在点，使的面积等于的面积的一半仍然成立，若存在，直接写出其他符合条件的点的坐标；

（3）如图2，过点作轴交轴于点，点为线段延长线上一动点，连接，平分，，当点运动时，求证：

Answer 1

【答案】（1）m=-2，n=4；（2）①M的坐标为（3，0）；②（-3，0）或（0，6）或（0，-6）； （3）见解析

【解析】

（1）根据非负数的性质列出方程组，解方程组即可；
（2）①根据三角形的面积公式计算即可；
②分点M在x、y轴上两种情况计算；
（3）根据角平分线的定义、垂直的定义得到∠POF=∠BOF，设∠POF=∠BOF=x，∠DOE=y，结合图形得到x=y，得到答案．

解：（1）由题意得，，

解得m=-2，n=4；

（2）①设点M的坐标的坐标为（x，0），

△ABC的面积= ×6×2=6，

由题意得，×x×2=×6，

解得，x=3，

△COM的面积等于△ABC的面积的一半时，点M的坐标为（3，0）；

②当点M在x轴上时，由①得，点M的坐标为（3，0）或（-3，0），
当点M在y轴上时，设点M的坐标的坐标为（0，y），
由题意得，×|y|×1=×6，
解得，y=±6，
综上所述，符合条件的点M的其他坐标为（-3，0）或（0，6）或（0，-6）；

（3）∵OE平分∠AOP，
∴∠EOP=∠AOE，
∵OF⊥OE，
∴∠EOP+∠POF=90°，∠AOE+∠BOF=90°，
∴∠POF=∠BOF，
设∠POF=∠BOF=x，∠DOE=y，
∵CD⊥y轴，
∴CD∥x轴，
∴∠OPD=∠POB=2x，
则∠POD=90°-2x，
∵∠EOF=90°，
∴y+90°-2x+x=90°，
解得，x=y，
∴∠OPD=2∠DOE.