题目内容
根据tan30°=
| ||
| 3 |
| 3 |
| 1 | ||
2+
|
| 3 |
分析：利用正切值等于对边比邻边，构造直角三角形求解．
解答：
解：作∠A=45°，AB=
，AC=BC=1，
延长CA至点D，使AD=AB，连接BD．
则tanD=tan22.5°=
=
-1．
解：作∠A=45°，AB=| 2 |
延长CA至点D，使AD=AB，连接BD．
则tanD=tan22.5°=
| 1 | ||
1+
|
| 2 |
点评：本题是信息题，由题中给出求tan15°的方法，构造出能求tan22.5°的值的直角三角形求解，关键构造出△BAD是等腰三角形，而∠BAC为45°，又为△BAD的外角，所以∠D=22.5，再由正切的定义求出tan22.5°的值．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
（1）计算：
构造△ABC，使∠A=30°，AB=2，BC=1，AC=
，再延长CA到点D，使AB=AD，连接BD，则tan15°=
=2-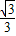
构造△ABC，使∠A=30°，AB=2，BC=1，AC=
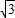，再延长CA到点D，使AB=AD，连接BD，则tan15°=
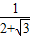=2-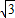
，同样根据tan45°=1，模仿前面的做法求出tan22.5°的值．
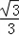，构造△ABC，使∠A=30°，AB=2，BC=1，AC=
，再延长CA到点D，使AB=AD，连接BD，则tan15°=
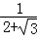=2﹣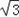
，同样根据tan45°=1，模仿前面的做法求出tan22.5 °的值。