Question

如图，在直角坐标系中，O是坐标原点，点C的坐标是（0，3），抛物线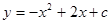经过点C，交x轴负半轴于点A．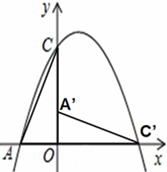

（1）求c的值，并写出抛物线解析式；
（2）将△AOC绕点O顺时针旋转90°，得到△A’OC’．
①求点C’的坐标，并通过计算判断点C’是否在抛物线上；
②若将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△A’OC’的内部（不包括△A’OC’的边界），求m的取值范围（直接写出答案即可）．

Answer 1

（1）c=3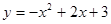，；（2）在；（3）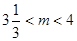

解析试题分析：（1）把（0，3）代入抛物线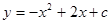即可得到结果；
（2）①先根据旋转的性质求得点C’的坐标，再代入函数关系式即可判断；
②先求出点A的坐标，根据旋转的性质可得点A’的坐标，从而得到直线A’ C’的函数关系式，再求出抛物线的顶点坐标，最后根据向下平移抛物线顶点落在△A’OC’的内部即可分情况讨论.
（1）把C（0，3）代入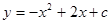，得c="3"
∴抛物线解析式为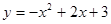 
（2）∵OC=3   
∴OC’=3
∴C’坐标为（3，0）      
当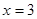时，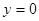
∴点C’在抛物线上；
（3）.
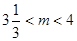考点：本题考查的是二次函数的性质，旋转的性质
点评：解答本题的关键是熟记旋转的性质：旋转前后的对应点到旋转中心的距离相等；同时熟练掌握求二次函数顶点坐标的方法：公式法或配方法.