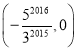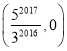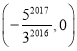Question

【题目】如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC垂足为E.

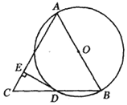
(1)求证：AB=AC；

(2)若⊙O半径为5，∠BAC=60°，求DE的长.

Answer 1

【答案】（1）见解析；（2）DE=.

【解析】

（1）连接AD，由AB是直径，可知∠ADB=90°，在△ABC中，BD=CD，可知AD是中垂线，所以AB=AC；

（2）由题意易得△ABC是等边三角形，所以CD等于半径，在Rt△CDE中，利用60°的三角函数可求出DE.

（1）连接AD

∵AB是⊙O的直径,∴∠ADB=90°,

又∵BD=CD，∴AD是BC的垂直平分线，∴AB=AC.

（2）由AB=AC，∠BAC=60°知△ABC是等边三角形

∵⊙O的半径为5，∴AB=BC=10，CD=BC=5，又∠C=60°，

∴DE=CD·sin60°=.