题目内容
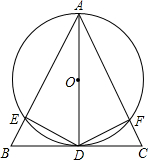 (2013•松北区三模)如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙0与AB、AC两边分别交于点E、F.连接DE、DF.
(2013•松北区三模)如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙0与AB、AC两边分别交于点E、F.连接DE、DF.(1)求证:BE=CF;
(2)若AD=BC=2
| 5 |
分析:(1)根据等腰三角形“三合一”的性质推知∠1=∠2.由“直径所对的圆周角是直角”得到∠AED=∠AFD=90°.则根据角平分线的性质证得结论;
(2)在直角△ABD中利用勾股定理求得斜边AB的长度,然后根据面积法来求ED的长度.
(2)在直角△ABD中利用勾股定理求得斜边AB的长度,然后根据面积法来求ED的长度.
解答: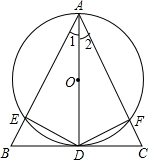 (1)证明:如图,∵在△ABC中,AB=AC,AD为△ABC的高,
(1)证明:如图,∵在△ABC中,AB=AC,AD为△ABC的高,
∴∠1=∠2.
又∵AD为直径,
∴∠AED=∠AFD=90°,即DE⊥AB,DF⊥AC,
∴DE=DF;
(2)如图,∵在△ABC中,AB=AC,AD为△ABC的高,AD=BC=2
.
∴BD=CD=
BC=
.
∴由勾股定理得到AB=
=5.
∵由(1)知DE⊥AB,
∴
AD•BD=
AB•ED,
∴ED=
=
=2.
 (1)证明:如图,∵在△ABC中,AB=AC,AD为△ABC的高,
(1)证明:如图,∵在△ABC中,AB=AC,AD为△ABC的高,∴∠1=∠2.
又∵AD为直径,
∴∠AED=∠AFD=90°,即DE⊥AB,DF⊥AC,
∴DE=DF;
(2)如图,∵在△ABC中,AB=AC,AD为△ABC的高,AD=BC=2
| 5 |
∴BD=CD=
| 1 |
| 2 |
| 5 |
∴由勾股定理得到AB=
| AD2+BD2 |
∵由(1)知DE⊥AB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴ED=
| AD•BD |
| AB |
2
| ||||
| 5 |
点评:本题考查了等腰三角形的性质、勾股定理.注意,勾股定理应用于直角三角形中.

练习册系列答案
相关题目
 (2013•松北区三模)如图是某个几何体的三视图,则该几何体是( )
(2013•松北区三模)如图是某个几何体的三视图,则该几何体是( )