题目内容
已知：实数a，b在数轴上的位置如图所示，化简：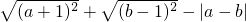
解：如图，∵-1＜a＜0，1＜b，
∴a+1＞0，b-1＞0，a-b＜0，
∴原式=|a+1|+|b-1|-|a-b|
=（a+1）+（b-1）-（b-a）
=2a．
分析：由a、b在数轴上的位置，即得：a+1＞0，b-1＞0，a-b＜0，然后即可对二次根式进行化简，再根据绝对值的定义去绝对值号．
点评：本题主要考查实数与数轴的关系、二次根式的性质与化简，关键在于通过a、b在数轴上的位置关系，推出啊、b的取值范围．
∴a+1＞0，b-1＞0，a-b＜0，
∴原式=|a+1|+|b-1|-|a-b|
=（a+1）+（b-1）-（b-a）
=2a．
分析：由a、b在数轴上的位置，即得：a+1＞0，b-1＞0，a-b＜0，然后即可对二次根式进行化简，再根据绝对值的定义去绝对值号．
点评：本题主要考查实数与数轴的关系、二次根式的性质与化简，关键在于通过a、b在数轴上的位置关系，推出啊、b的取值范围．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
中y的值随x的增大而增大。⑥已知点P（
，
）在函数
的图象上，那么点P应在平面直角坐标系中的第二象限。
中y的值随x的增大而增大。⑥已知点P（
，
）在函数
的图象上，那么点P应在平面直角坐标系中的第二象限。
）个 
第三象限，③除了用有序实数对，我们也可以用方向和距离来确定物体的位置，④若点P的坐标为（a，b），且ab=0，则P点是坐标原点，⑤函数
中y的值随x的增大而增大。⑥已知点P（
，
的图象上，那么点P应在平面直角坐标系中的第二象限。
）个 
第三象限，③除了用有序实数对，我们也可以用方向和距离来确定物体的位置，④若点P的坐标为（a，b），且ab=0，则P点是坐标原点，⑤函数
中y的值随x的增大而增大。⑥已知点P（
，
的图象上，那么点P应在平面直角坐标系中的第二象限。