��Ŀ����
����Ŀ��ij��ѧ������֯ѧ����չ�����Ķ����Ϊ�˽ⱾУ1500��ѧ��ÿ�ܿ����Ķ���ʱ����t����λ��Сʱ����������������ķ�����ȡ����ѧ���������ʾ����飬��������0��t��2��2��t��3��3��t��4��t��4��Ϊ�ĸ��ȼ������ֱ���A��B��C��D��ʾ�����ݵ�����ͳ�����ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ�и�������Ϣ����������⣺
��1�����������������������
��2��x= �� ����������������ͳ��ͼ����������
��3��������t��3������Ϊ�ϸ���ô���Ƹ���ѧÿ�ܿ����Ķ�ʱ�����ϸ������Ƕ��٣�
���𰸡�
��1��200
��2��30
��3���⣺1500����10%+15%��=375���ˣ���
�������ѧÿ�ܿ����Ķ�ʱ�����ϸ�������375�ˣ�
���������⣺��1����������ã�90��45%=200��������
���������������������200��
���Դ��ǣ�200����2����������ã�x%=1����45%+10%+15%��=30%����x=30��
�ߵ����������Ϊ90��45%=200���ˣ���
��B�ȼ�����Ϊ200��30%=60���ˣ���
C�ȼ�����Ϊ200��10%=20���ˣ���
��ͼ��
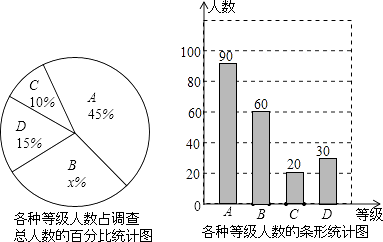
��1���ɵȼ�A����������ռ�İٷֱȵõ��������������ɣ�
��2����������ͳ��ͼ���x��ֵ�����ݵ�������������ȼ�ΪB��C����������ȫ����ͳ��ͼ���ɣ�
��3�����ݵȼ�C��D�İٷֱ�֮�ͳ���1500���ɵõ������
�����㾫�����������塢���塢��������������������ͳ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��Ҫ�����ȫ���������壬��������ÿһ���������и��壬����ȡ���Dz��ָ�����������һ�������������и������Ŀ�������������������������û�е�λ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����


