题目内容
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A,O之间的距离为d。

1.如图1,当r<a时,根据d与a,r之间关系,请你将⊙O与正方形的公共点个数填入下表:
|
d,a,r之间的关系 |
公共点的个数 |
|
d>a+r |
0 |
|
d=a+r |
|
|
a-r<d<a+r |
|
|
d=a-r |
|
|
d<a-r |
|
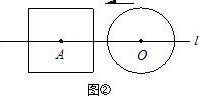
2.如图2,当r=a时,根据d与a,r之间关系,请你写出⊙O与正方形的公共点个数,即当r=a时,⊙O与正方形的公共点个数可能有 个。

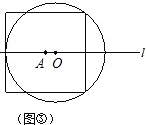
3.如图3,当⊙O与正方形的公共点个数有5个时,r= (请用a的代数式表示r,不必说明理由)。

1.如图①
|
d、a、r之间关系 |
公共点的个数 |
|
d>a+r |
0 |
|
d=a+r |
1 |
|
a-r<d<a+r |
2 |
|
d=a-r |
1 |
|
d<a-r |
0 |
所以,当r<a时,⊙O与正方形的公共点的个数可能有0、1、2个;(4分)
2.如图②
|
d、a、r之间关系 |
公共点的个数 |
|
d>a+r |
0 |
|
d=a+r |
1 |
|
a≤d<a+r |
2 |
|
d<a |
4 |
所以,当r=a时,⊙O与正方形的公共点个数可能有0、1、2、4个;(8分)
3.如图③所示,连接OC.
则OE=OC=r,OF=EF-OE=2a-r.
在Rt△OCF中,由勾股定理得:
OF2+FC2=OC2
即(2a-r)2+a2=r2,
4a2-4ar+r2+a2=r2,
5a2=4ar,
R= ;(12分)
;(12分)
【解析】(1)当r<a时,⊙A的直径小于正方形的边长,⊙A与正方形中垂直于直线l的一边相离、相切、相交,三种情况,故可确定⊙O与正方形的交点个数;
(2)当r=a时,⊙O的直径等于正方形的边长,此时会出现⊙A与正方形相离,与正方形一边相切,相交,与正方形四边相切,四种情况,故可确定⊙O与正方形的交点个数;
(3)如图③,当⊙O与正方形有5个公共点时,连接OC,用a、r表示△COF的各边长,在Rt△OCF中,由勾股定理求a、r的关系.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:

| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
d=a+r |
|
| a≤d<a+r | |
| d=a-r | |
| d<a-r |
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a |
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
| 5 |
| 4 |
(4)就r>a的情形,请你仿照“当…时,⊙O与正方形的公共点个数可能有
(注:第(4)小题若多给出一个正确结论,则可多得2分,但本大题得分总和不得超过12分).
(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间的关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a-r<d<a+r | |
| d=a-r | |
| d<a-r |
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间的关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a |

所以,当r=a时,⊙O与正方形的公共点个数可能有
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
| 5 |
| 4 |


(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a-r<d<a+r | |
| d=a-r | |
| d<a-r |
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a |
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
| 5 |
| 4 |




