题目内容
如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O′,交 轴的负半轴于点C,则点C的坐标为 ,若二次函数
轴的负半轴于点C,则点C的坐标为 ,若二次函数 的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标
的图像经过点A,C,B.已知点P是该抛物线上的动点,当∠APB是锐角时,点P的横坐标 的取值范围是 .
的取值范围是 .
【答案】
(0,-4),0<x<6
【解析】
试题分析:根据已知条件,得出圆的方程为
令x=0,得出 ,因为点C在x轴下方,所以得出C点坐标为(0,-4)
,因为点C在x轴下方,所以得出C点坐标为(0,-4)
抛物线与X州交于点A(-2,0),B(8,0),抛物线方程为 。代入三个点的坐标,得出抛物线方程
。代入三个点的坐标,得出抛物线方程 ,抛物线的顶点在 (
,抛物线的顶点在 ( ,
, ),也就是,对称轴x=3,开口向上的抛物线,
),也就是,对称轴x=3,开口向上的抛物线,
因为直径所对的角是圆周角,所以,∠ACB是直角
C坐标(0,-4)关于X=3对称点坐标是(6,-4)
当∠APB是锐角时,点P的横坐标 的取值范围是0<x<6
的取值范围是0<x<6
考点:圆的综合应用以及坐标系内求点的坐标,抛物线顶点和动点问题
点评:难度系数较大,特别注意对抛物线的顶点,对称轴的利用,对于圆周角性质的理解,数形结合,得出结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )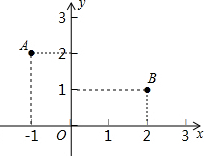 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )