题目内容
(2012•鼓楼区一模)在弹性程度内,一根弹簧最大可伸长长度为58cm.如图是由三根相同的上述弹簧构成的拉力器, 已知拉力y与弹簧的总长度x之间是一次函数的关系,函数y与自变量x的部分对应值如下表:
已知拉力y与弹簧的总长度x之间是一次函数的关系,函数y与自变量x的部分对应值如下表:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求拉力y的最大值;
(3)已知某儿童最大拉力为400N,求该儿童能使单根弹簧伸长的最大长度.
 已知拉力y与弹簧的总长度x之间是一次函数的关系,函数y与自变量x的部分对应值如下表:
已知拉力y与弹簧的总长度x之间是一次函数的关系,函数y与自变量x的部分对应值如下表:| x(单位:cm) | 28 | 30 | 35 |
| y(单位:N) | 0 | 120 | 420 |
(2)求拉力y的最大值;
(3)已知某儿童最大拉力为400N,求该儿童能使单根弹簧伸长的最大长度.
分析:(1)利用待定系数法即可求得函数的解析式,以及x的范围;
(2)拉力y是总长度x的函数,根据一次函数的性质,即可确定y的最大值;
(3)首先求得一根弹簧每伸长1 cm,需用的力的大小,然后用400N除以弹簧每伸长1cm需用的力的大小即可求解.
(2)拉力y是总长度x的函数,根据一次函数的性质,即可确定y的最大值;
(3)首先求得一根弹簧每伸长1 cm,需用的力的大小,然后用400N除以弹簧每伸长1cm需用的力的大小即可求解.
解答:解:(1)设y=kx+b(k≠0),根据题意得:
解得:
,
所以y与x之间的函数关系式为:y=60x-1680.
自变量x的取值范围为:28≤x≤58.
(2)当x=58时,y=60×58-1680=1800,所以拉力最大值为1800 N.
(3)三根弹簧每伸长1cm,需用力60N,一根弹簧每伸长1cm,需用力20N,
400÷20=20cm.
所以最大可使单根弹簧的长度伸长20cm.
|
解得:
|
所以y与x之间的函数关系式为:y=60x-1680.
自变量x的取值范围为:28≤x≤58.
(2)当x=58时,y=60×58-1680=1800,所以拉力最大值为1800 N.
(3)三根弹簧每伸长1cm,需用力60N,一根弹簧每伸长1cm,需用力20N,
400÷20=20cm.
所以最大可使单根弹簧的长度伸长20cm.
点评:本题考查了一次函数的应用,能够熟练找到题目中的等量关系和不等关系分别列方程和不等式进行求解.同时要注意和函数的结合分析,利用函数的单调性来求最值问题是常用的方法要掌握.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
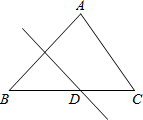 (2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )
(2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )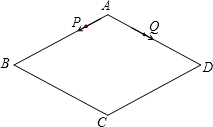 /s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
/s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.