题目内容
如图，在⊙O中，直径CD垂直弦AB于点E，连接OB，CB，已知⊙O的半径为2，AB=
，则∠BCD=________度．
30
分析：首先在直角三角形OEB中利用锐角三角函数求得∠EOB的度数，然后利用同弧所对的圆心角和圆周角之间的关系求得∠BCD的度数即可．
解答：∵直径CD垂直弦AB于点E，AB=，
∴EB=
AB=
，
∵⊙O的半径为2，
∴sin∠EOB=
，
∴∠EOB=60°，
∴∠BCD=30°．
故答案为30．
点评：本题考查了垂径定理及特殊角的三角函数值，解题的关键是利用垂径定理得到直角三角形．
分析：首先在直角三角形OEB中利用锐角三角函数求得∠EOB的度数，然后利用同弧所对的圆心角和圆周角之间的关系求得∠BCD的度数即可．
解答：∵直径CD垂直弦AB于点E，AB=
，∴EB=
AB=，∵⊙O的半径为2，
∴sin∠EOB=
，∴∠EOB=60°，
∴∠BCD=30°．
故答案为30．
点评：本题考查了垂径定理及特殊角的三角函数值，解题的关键是利用垂径定理得到直角三角形．
练习册系列答案
相关题目
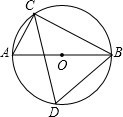如图，在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，则BC=
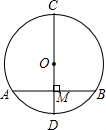如图，在⊙O中，直径CD的长度为10cm，AB是弦，且AB⊥CD于M，OM=3cm，求弦AB的长．
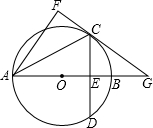C与直线AB相交于点G．
（2013•百色）如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠ABO的度数是（ ）
（2012•朝阳区二模）如图，在⊙O中，直径AB⊥弦CD于点H，E是⊙O上的点，若∠BEC=25°，则∠BAD的度数为（ ）