题目内容
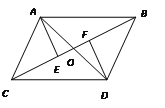
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
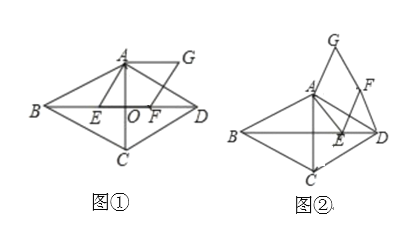
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)AE=BE;(2)成立,理由见解析
【解析】
(1)先根据题意判断![]() 是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
(2)先判断出△ACD和△AEF是等边三角形,进而得出∠CAE=∠DAF,即可判断出△ACE≌△ADF,即可得出结论.
(1)如图,连接AF,
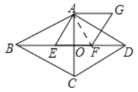
∵![]() ,且
,且![]() ,
,
∴四边形ABCD是菱形,
∴AC⊥BD,∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
∴∠OAE=∠OAF=30°,
∴∠DAF=30°=∠ADO,
∴AF=FD,
∵AF=EF,
∴EF=FD;
∵∠AEF=60°,
∴∠BAE=30°=∠ABO,
∴AE=BE.
(2)成立,如图,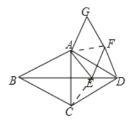
连接CE,AF,
∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AD=CD,AE=EF,BD垂直平分AC,∠ABC=∠ADC=60°,
∴∠ADC=∠AEF=60°,
∴△ACD和△AEF是等边三角形,
∴AC=AD,AE=AF=EF,∠CAD=∠EAF=60°,
∴∠CAE=∠DAF,
在△ACE和△ADF中, 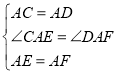 ,
,
△ACE≌△ADF(SAS),
∴EC=DF,
∵BD垂直平分AC,
∴EC=AE,
∴DF=AE=EF

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目