Question

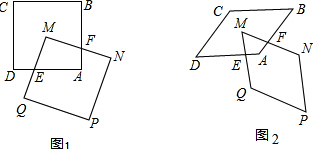
如图1，正方形ABCD和正方形QMNP，∠M=∠B，点M是正方形ABCD的对称中心，MN交AB于点F，QM交AD于点E．
（1）求证：ME=MF；
（2）如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．

Answer 1

分析：（1）过点M作MG⊥AB于G，作MH⊥AD于H，根据正方形的性质可得MG=MH，∠GMH=90°，再根据同角的余角相等求出∠EMH=∠FMG，然后利用“角边角”证明△EMH和△FMG全等，根据全等三角形对应边相等可得ME=MF；
（2）过点M作MG⊥AB于G，作MH⊥AD于H，根据菱形的性质可得MG=MH，再根据四边形的内角和定理求出∠GMH+∠A=180°，根据菱形的邻角互补求出∠B+∠A=180°，然后求出∠EMH=∠FMG，然后利用“角边角”证明△EMH和△FMG全等，根据全等三角形对应边相等可得ME=MF．

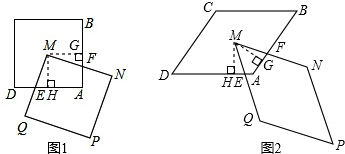
解答：（1）证明：如图1，过点M作MG⊥AB于G，作MH⊥AD于H，
∵M是正方形ABCD的对称中心，
∴MG=MH，∠GMH=90°，
∵∠EMH+∠FMH=90°，∠FMG+∠FMH=90°，
∴∠EMH=∠FMG，
在△EMH和△FMG中，

∠EMH=∠FMG MG=MH ∠MHE=∠FMG=90°

，
∴△EMH≌△FMG（ASA），
∴ME=MF；

（2）如图2，过点M作MG⊥AB于G，作MH⊥AD于H，
∵M是正方形ABCD的对称中心，
∴MG=MH，
∵∠GMH+∠A=360°-90°-90°=180°，
∠A+∠B=180°，
∴∠B=∠GMH，
∴∠EMF=∠GMH，
∵∠EMF=∠FMG+∠EMG，
∠GMH=∠EMH+∠EMG，
∴∠EMH=∠FMG，
在△EMH和△FMG中，

∠EMH=∠FMG MG=MH ∠MHE=∠FMG=90°

，
∴△EMH≌△FMG（ASA），
∴ME=MF．

点评：本题考查了正方形的性质，全等三角形的判定与性质，菱形的性质，作辅助线构造出全等三角形，再根据正方形、菱形的中心到各边的距离相等求出ME=MF是解题的关键．