题目内容
 如图所示,四边形ABCD内接于⊙O,则下列结论错误的是
如图所示,四边形ABCD内接于⊙O,则下列结论错误的是
- A.∠1=∠A
- B.∠B=∠D
- C.∠A+∠2=180°
- D.∠A+∠2=∠B+∠D
B
分析:根据圆内接四边形的性质可知,圆内接四边形对角互补,任何一个内角都等于它不相邻的内角,即可得出答案.
解答:A、∠1=∠A,根据圆内接四边形的性质可知:∠1=∠A,故此选项正确;
B、∠B=∠D,根据圆内接四边形的性质可知:∠B+∠D=180°,故此选项错误;
C、∠A+∠2=180°根据邻补角的定义得出∠A+∠2=180°,故此选项正确;
D、∠A+∠2=∠B+∠D,根据圆内接四边形的性质可知:∠1=∠A,故此选项正确.
故选B.
点评:此题主要考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解决问题的关键.
分析:根据圆内接四边形的性质可知,圆内接四边形对角互补,任何一个内角都等于它不相邻的内角,即可得出答案.
解答:A、∠1=∠A,根据圆内接四边形的性质可知:∠1=∠A,故此选项正确;
B、∠B=∠D,根据圆内接四边形的性质可知:∠B+∠D=180°,故此选项错误;
C、∠A+∠2=180°根据邻补角的定义得出∠A+∠2=180°,故此选项正确;
D、∠A+∠2=∠B+∠D,根据圆内接四边形的性质可知:∠1=∠A,故此选项正确.
故选B.
点评:此题主要考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解决问题的关键.

练习册系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )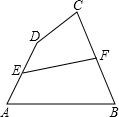 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
