题目内容
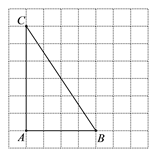
【题目】如图，在正方形网格中，每个小正方形的边长为1个单位长度．△ABC的三个顶点都在格点上.
⑴ 在线段AC上找一点P（不能借助圆规），使得
，画出点P的位置，并说明理由．
⑵ 求出⑴中线段PA的长度.
【答案】(1)详见解析；（2）线段PA的长度为
.
【解析】试题分析：
（1）利用方格纸可作出BC的垂直平分线交AC于点P，点P为所求的点，由线段垂直平分线的性质和勾股定理即可证明此时：PC2-PA2=AB2；
（2）由图中信息可得AB=4，AC=6，设PA= 
，则PC=PB=6- 
，在Rt△PAB中，由勾股定理建立方程解出
即可.
试题解析：
⑴ 如图，利用方格纸作BC的垂直平分线，分别交AC、BC于点P、Q，则PC＝PB.
∵在△APB中，∠A＝90°，
∴
，即： 
，
∴
.
⑵ 由图可得：AC=6，AB=4，设PA=x，则PB=PC=6－x
∵在△PAB中，∠A＝90°，
∴
，解得： 
，即PA=
.
答：线段PA的长度为
.
练习册系列答案
相关题目
