题目内容
(2012•大庆)在直角坐标系中,C(2,3),C′(-4,3),C″(2,1),D(-4,1)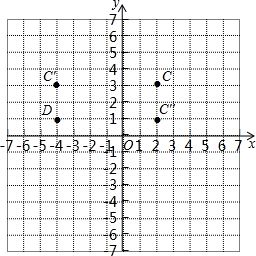 ,A(0,a),B(a,O)(a>0).
,A(0,a),B(a,O)(a>0).
(1)结合坐标系用坐标填空.
点C与C′关于点
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.
 ,A(0,a),B(a,O)(a>0).
,A(0,a),B(a,O)(a>0).(1)结合坐标系用坐标填空.
点C与C′关于点
(-1,3)
(-1,3)
对称; 点C与C″关于点(2,2)
(2,2)
对称;点C与D关于点(-1,2)
(-1,2)
对称;(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.
分析:(1)根据对称的性质,分别找出两对称点连线的中点即可;
(2)先求出点P的坐标,再利用△APB所在的梯形的面积减去两个直角三角形的面积,然后列式计算即可得解.
(2)先求出点P的坐标,再利用△APB所在的梯形的面积减去两个直角三角形的面积,然后列式计算即可得解.
解答: 解:(1)由图可知,点C与C′关于点(-1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(-1,2)对称;
解:(1)由图可知,点C与C′关于点(-1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(-1,2)对称;
故答案为:(-1,3),(2,2),(-1,2);
(2)点C关于点(4,2)的对称点P(6,1),
△PAB的面积=
(1+a)×6-
a2-
×1×(6-a)=5,
整理得,a2-7a+10=0,
解得a1=2,a2=5,
所以,a的值为2或5.
 解:(1)由图可知,点C与C′关于点(-1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(-1,2)对称;
解:(1)由图可知,点C与C′关于点(-1,3)对称; 点C与C″关于点(2,2)对称;点C与D关于点(-1,2)对称;故答案为:(-1,3),(2,2),(-1,2);
(2)点C关于点(4,2)的对称点P(6,1),
△PAB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得,a2-7a+10=0,
解得a1=2,a2=5,
所以,a的值为2或5.
点评:本题考查了坐标与图形的变化-对称,以及坐标与图形的性质,明确两点关于这两点连线的中点对称是解题的关键,(2)中△PAB的面积用所在梯形的面积减去两个直角三角形的面积表示是解题的关键.

练习册系列答案
相关题目
 (2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
(2012•大庆)如图所示,将一个圆盘四等分,并把四个区域分别标上I、Ⅱ、Ⅲ、Ⅳ,只有区域I为感应区域,中心角为60°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( ) (2012•大庆)实数a、b在数轴上对应点的位置如图所示,则下列各式正确的是( )
(2012•大庆)实数a、b在数轴上对应点的位置如图所示,则下列各式正确的是( ) 动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.
动,第一次回到点A处停止运动,设AP=S,用t表示运动时间.