��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A��6��0����B��0��8������C������Ϊ��0��m��������C��CE��AB�ڵ�E����DΪx���ϵ�һ���㣬����CD��DE����CD��DEΪ����CDEF��
��1����0��m��8ʱ����CE�ij����ú�m�Ĵ���ʽ��ʾ����
��2����m=3ʱ���Ƿ���ڵ�D��ʹCDEF�Ķ���Fǡ������y���ϣ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3����D�������˶������У�������Ψһ��λ�ã�ʹ��CDEFΪ���Σ��������������������m��ֵ��
���𰸡�
��1��
�⣺��A��6��0����B��0��8����
��OA=6��OB=8��
��AB=10��
�ߡ�CEB=��AOB=90�㣬
�֡ߡ�OBA=��EBC��
���BCE�ס�BAO��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��CE= ![]() ��
�� ![]() m
m
��2��
�⣺��m=3��
��BC=8��m=5��CE= ![]() ��
�� ![]() m=3��
m=3��
��BE=4��
��AE=AB��BE=6��
�ߵ�F����y���ϣ���ͼ2����

��DE��BO��
���EDA�ס�BOA��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
��OD= ![]() ��
��
���D�������� ![]() ��0��
��0��
��3��
�⣺ȡCE���е�P����P��PG��y���ڵ�G��
��CP= ![]() CE=
CE= ![]() ��
�� ![]() m��
m��
����m��0ʱ��
�ٵ�0��m��8ʱ����ͼ3����֤��GCP=��BAO��
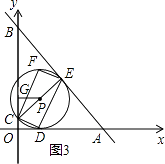
��cos��GCP=cos��BAO= ![]() ��
��
��CG=CPcos��GCP= ![]() ��
�� ![]() ��
�� ![]() m��=
m��= ![]() ��
�� ![]() m��
m��
��OG=OC+CG=m+ ![]() ��
�� ![]() m=
m= ![]() m+
m+ ![]() ��
��
��������ã��ã�OG=CP��
�� ![]() m+
m+ ![]() =
= ![]() ��
�� ![]() m��
m��
��ã�m= ![]() ��
��
�ڵ�m��8ʱ��OG��CP����Ȼ����������������m��ֵ��
����m=0ʱ������C��ԭ��O�غϣ���ͼ4����
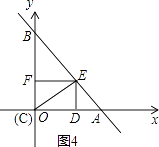
����m��0ʱ��
�ٵ���E���A�غ�ʱ������ͼ5����
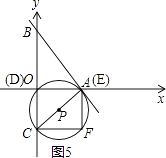
��֤��COA�ס�AOB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��ã�m=�� ![]() ��
��
�ڵ���E���A���غ�ʱ������ͼ6����
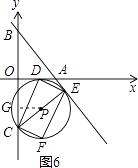
OG=OC��CG=��m���� ![]() ��
�� ![]() m��
m��
=�� ![]() m��
m�� ![]() ��
��
������ã�OG=CP��
�ੁ ![]() m��
m�� ![]() =
= ![]() ��
�� ![]() m��
m��
���m=�� ![]() ��
��
����������m��ֵ�� ![]() ��0��
��0�� ![]() ��
�� ![]() ��
��
����������1������֤����BCE�ס�BAO���������������εĶ�Ӧ�ߵı���ȼ�����ã���2��֤����EDA�ס�BOA���������������εĶ�Ӧ�ߵı���ȼ�����ã���3����m��0��m=0��m��0��������������ۣ���m=0ʱ��һ����������m��0ʱ����0��m��8��m��8����������������Ǻ����Ķ��弴����⣮��m��0ʱ���ֵ�E���A�غϺ͵�E���A���غ�ʱ����������������ۣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�





