题目内容
10.在△ABC中,$(3-\frac{\sqrt{3}}{tanA})^{2}$+|2cos(90°-∠B)-1|=0,则△ABC为( )| A. | 直角三角形 | B. | 等边三角形 | ||
| C. | 含60°角的任意三角形 | D. | 顶角是钝角的等腰三角形 |
分析 根据非负数的性质可得:3-$\frac{\sqrt{3}}{tanA}$=0,2cos(90°-∠B)-1=0,据此求出∠A和∠B的度数,然后判断△ABC的形状.
解答 解:由题意得,3-$\frac{\sqrt{3}}{tanA}$=0,2cos(90°-∠B)-1=0,
∴tanA=$\frac{\sqrt{3}}{3}$,cos(90°-∠B)=$\frac{1}{2}$,
∴∠A=30°,∠B=30°,
则∠C=180°-30°-30°=120°,
即△ABC为顶角是钝角的等腰三角形.
故选D.
点评 本题考查了特殊角的三角函数值,解答本题的关键是根据非负数的性质得出tanA=$\frac{\sqrt{3}}{3}$,cos(90°-∠B)=$\frac{1}{2}$.

练习册系列答案
相关题目
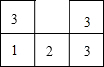 如图是从上面看由一些小正方体搭成的几何体的视图.正方形中的数字表示在该位置小正方体的个数.
如图是从上面看由一些小正方体搭成的几何体的视图.正方形中的数字表示在该位置小正方体的个数.