题目内容
方程(3-2x)2+(2x-3)=0的解是
- A.x1=1,x2=

- B.x1=-1,x2=

- C.x1=
 ,x2=
,x2=
- D.x1=
 ,x2=
,x2=
A
分析:方程的左边比较容易分解因式,因而利用因式分解法解方程比较简单.
解答:方程可以变形为:(2x-3)(2x-3+1)=0
则2x-3=0或2x-3+1=0
解得:x1=1,x2=
故选A.
点评:注意因式分解法解一元二次方程的依据,理解因式分解法的基本思想是降次.
分析:方程的左边比较容易分解因式,因而利用因式分解法解方程比较简单.
解答:方程可以变形为:(2x-3)(2x-3+1)=0
则2x-3=0或2x-3+1=0
解得:x1=1,x2=

故选A.
点评:注意因式分解法解一元二次方程的依据,理解因式分解法的基本思想是降次.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
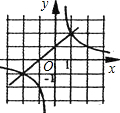 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y=