题目内容
 如图,等边△ABC中,AB=3,P为BC上一点,D为AC上一点,若BP=l,CD=
如图,等边△ABC中,AB=3,P为BC上一点,D为AC上一点,若BP=l,CD= ,则∠APD等于
,则∠APD等于
- A.30°
- B.45°
- C.60°
- D.不确定
C
分析:考查相似三角形的应用,题中△ABP∽△PCD,然后得出∠ABP与∠CPD的和,进而可求出∠APD的大小.
解答:由题意得,∠B=∠C,
 =
= ,
,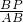 =
=
∴ =
=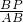 ,
,
∴△ABP∽△PCD,
∴∠CPD=∠BAP,
∵∠BPA+∠BAP=120°,∴∠BPA+∠DPC=120°
∴∠APD=60°
故选C.
点评:熟练掌握等边三角形的性质,会用相似三角形求解一些简单的计算问题.
分析:考查相似三角形的应用,题中△ABP∽△PCD,然后得出∠ABP与∠CPD的和,进而可求出∠APD的大小.
解答:由题意得,∠B=∠C,
 =
= ,
,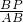 =
=
∴
 =
=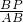 ,
,∴△ABP∽△PCD,
∴∠CPD=∠BAP,
∵∠BPA+∠BAP=120°,∴∠BPA+∠DPC=120°
∴∠APD=60°
故选C.
点评:熟练掌握等边三角形的性质,会用相似三角形求解一些简单的计算问题.

练习册系列答案
相关题目

 如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF. 如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF. 如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数.
如图,等边△ABC中,D是BC上一点,以AD为边作等腰△ADE,使AD=AE,∠DAE=80°,DE交AC于点F,∠BAD=15°,求∠FDC的度数. 如图,等边△ABC中,AD=CE,BD和AE相交于F,BG⊥AE垂足为G,求∠FBG的度数.
如图,等边△ABC中,AD=CE,BD和AE相交于F,BG⊥AE垂足为G,求∠FBG的度数.